动态规划算法是解决复杂问题的一个方法，该方法把复杂问题分解为子问题，通过求解子问题进而得到整个问题的解。在解决子问题的时候，其结果通常需要存储起来被用来解决后续复杂问题。当问题具有下列特性时，可以考虑使用动态规划来求解：

1. 最优子结构性质: 问题最优解包含子问题的解也是子问题的最优解 ；
2. 子问题重叠性质: 使用递归算法自顶向下对问题进行求解，每次产生的子问题并不总是新问题。

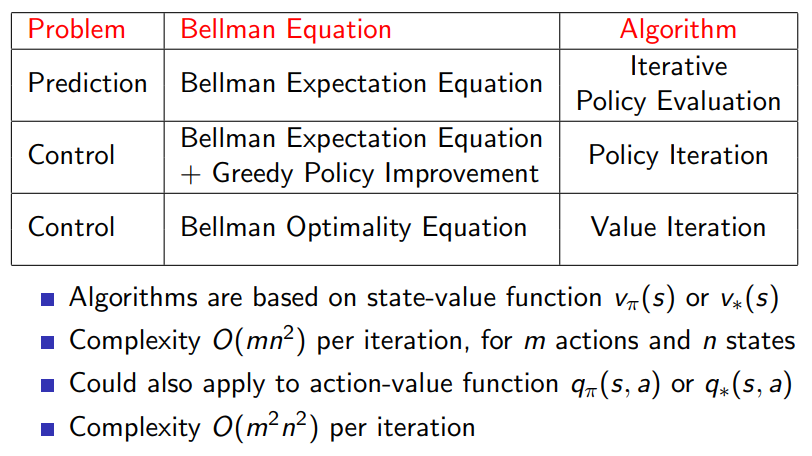
MDP 是满足以上两个属性的，贝尔曼方程具有递归形式，价值函数可以保存和重复利用 。在 MDP 中有两类问题，预测和控制。

预测： 给定一个 MDP $<S,\mathcal{A},\mathcal{P},\mathcal{R},\gamma>$ 和策略 $\pi$ ，输出价值函数 $V_\pi$ (评估)。

控制： 给定一个 MDP $<S,\mathcal{A},\mathcal{P},\mathcal{R},\gamma>$ ，求最优价值函数 $V_*$ 和 最优策略 $\pi_*$ 。

通常来讲 MDP 问题的求解最终都会对应到最优策略的选择上，因此一个直接的想法是，先任意给定一个策略，评估该策略，接着改进该策略，如此就能得到更好的策略。

策略评估

**问题：**评估一个给定的策略 $π$ ，即输出策略 $\pi$ 下各个状态的价值

**解决方案：**用贝尔曼期望方程进行迭代

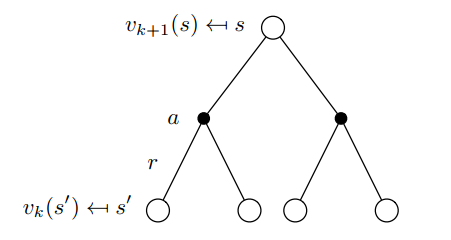
同步迭代：即在每次迭代过程中，对于第 $k+1$ 次迭代，所有的状态 $s$ 的价值 $V_{k+1}(s)$ 用 $V_k(s')$ 计算并更新，其中 $s’$ 是 $s$ 的后继状态。

$$ \begin{aligned} V_{k+1}(s) &=\sum_{a \in \mathcal{A}} \pi(a \mid s)\left(\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} v_{k}\left(s^{\prime}\right)\right) \\ \mathbf{V}^{k+1} &=\mathcal{R}^{\pi}+\gamma \mathcal{P}^{\pi} \mathbf{V}^{k} \end{aligned} $$ 异步迭代：状态更新单独进行(理论上任意顺序都可)，可以使用刚刚更新过的状态为前驱状态。

两种迭代方式最终都收敛到 $V_\pi$ 。

• 例子：方格世界

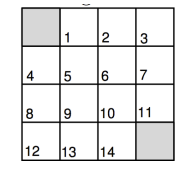
状态空间S： S1 - S14非终止状态，ST终止状态，下图灰色方格所示两个位置；

行为空间A： 对于任何非终止状态可以有东南西北移动四个行为；

**转移概率P：**任何试图离开方格世界的动作其位置将不会发生改变，其余条件下将100%地转移到动作指向的状态；

**即时奖励R：**任何在非终止状态间的转移得到的即时奖励均为 -1，进入终止状态即时奖励为0；

**衰减系数γ：**1；

**当前策略π：**Agent 采用随机行动策略，在任何一个非终止状态下有均等的几率采取任一移动方向这个行为，即 $π(n|•) = π(e|•) = π(s|•) = π(w|•) = 1/4$。

**问题：**评估在这个方格世界里给定的策略。

• 如何改善策略

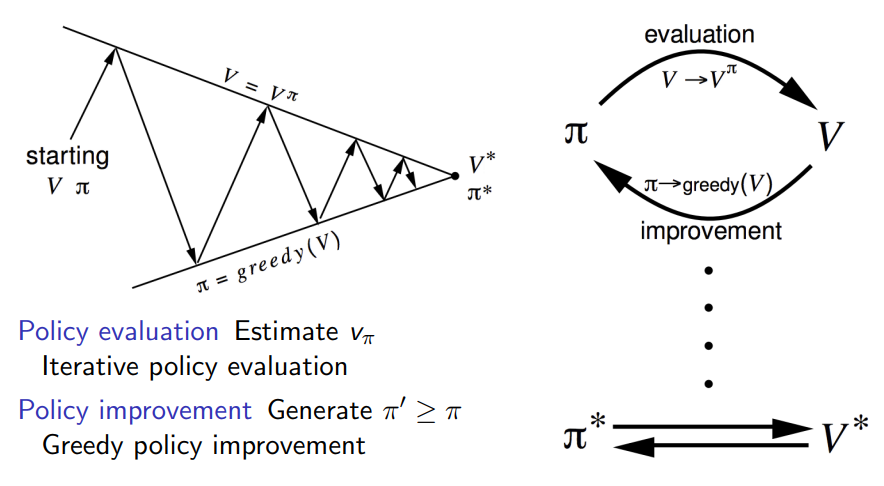
通过方格世界的例子，可得到了一个优化策略的办法，分为两步：

第一步进行 策略评估：在一个给定的策略下迭代更新价值函数：

$$V_\pi(s)=\mathbb{E}[\mathcal{R}_{t+1}+\gamma\mathcal{R}_{t+2}+\cdots\mid S_t=s]$$

第二步在当前策略基础上，贪婪地选取动作，进行 策略提升：

$$\pi^{\prime}=greedy(V_\pi)$$

循环一二步的过程直至收敛，这就是 策略迭代。

策略迭代

评估当前策略 $\pi$ 得到相应的价值 $V$，再根据 $V$ 进行贪婪地更新策略，如此反复，最终会收敛到最优策略 $\pi^*$ 和最优价值 $V^*$。

• 例子：汽车租赁

一个汽车租赁公司有两个地点提供汽车租赁，由于不同的店车辆租赁的市场条件不一样，为了能够实现利润最大化，该公司需要在每天下班后在两个租赁点转移车辆，以便第二天能最大限度的满足两处汽车租赁服务。

**状态空间：**2个地点，每个地点最多 20 辆车供租赁；

动作空间： 每天下班后最多从一处到另一处转移5辆车；

**即时奖励：**每租出 1 辆车奖励 10 元，必须是有车可租的情况；不考虑在两地转移车辆的支出；

转移概率： 租出去的车辆数量 $n$ 和归还的车辆数量 $n$ 是随机的，不过满足泊松分布 $P(X=n)=\frac{\lambda^n}{n!}e^{-\lambda}$ ，其中 1 号租车点租出去的车辆和还回来的车辆均服从 $\lambda = 3$ 的泊松分布， 2 号租车点租出去的车辆服从 $\lambda = 4$ 的泊松分布，还回来的车辆服从 $\lambda =2 $ 的泊松分布；

衰减系数： $\gamma=0.9$；

问题：最优策略是什么？

**求解方法：**选定一个随意的策略，如不管两地租赁业务市场需求，不移动车辆。然后开始策略迭代，直至收敛。(编程作业)

• 策略提升的理论证明

考虑一个确定性策略，$a=\pi(s)$，可以通过贪婪选取动作优化该策略：

$$\pi^{\prime}(s)=\arg\max_{a\in \mathcal{A}} Q_\pi(s,a)$$

该单步贪婪必然会提升在每个状态 $s$ 的动作价值，因：

$$Q_{\pi}\left(s, \pi^{\prime}(s)\right)=\max _{a \in \mathcal{A}} Q_{\pi}(s, a) \geq Q_{\pi}(s, \pi(s))=V_{\pi}(s)$$

贪婪过程持续下去，则会提升 $s$ 的状态价值，即 $V_{\pi^{\prime}}(s)\geq V_\pi(s)$ :

$$\begin{aligned} V_{\pi}(s) & \leq Q_{\pi}\left(s, \pi^{\prime}(s)\right)=\mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma V_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right] \\ & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma Q_{\pi}\left(S_{t+1}, \pi^{\prime}\left(S_{t+1}\right)\right) \mid S_{t}=s\right] \\ & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} Q_{\pi}\left(S_{t+2}, \pi^{\prime}\left(S_{t+2}\right)\right) \mid S_{t}=s\right] \\ & \leq \mathbb{E}_{\pi^{\prime}}\left[R_{t+1}+\gamma R_{t+2}+\ldots \mid S_{t}=s\right]=V_{\pi^{\prime}}(s) \end{aligned}$$

当提升停止时，对每个状态 $s$ 必有：

$$Q_{\pi}\left(s, \pi^{\prime}(s)\right)=\max _{a \in \mathcal{A}} Q_{\pi}(s, a)=Q_{\pi}(s, \pi(s))=V_{\pi}(s)$$

此时，贝尔曼最优方程满足：

$$V_{\pi}(s)=\max _{a\in \mathcal{A}} Q_{\pi}(s, a)$$

这意味着 $V_\pi(s)=V_*(s),\forall s\in S$ ，所以 $\pi$ 是最优策略。

思考： 在进行策略评估时，状态价值的收敛非常慢，是否有必要一定要迭代到状态价值收敛再执行策略提升呢？

答案是没必要，策略评估时状态价值没必要精确计算，因为通常只迭代几次就能发现更好的策略了。最极端的情况，策略评估时状态价值仅迭代一次后就执行策略提升，这样最终仍旧能够收敛到最优策略，这实际上等价于价值迭代 。

价值迭代

上文已说，价值迭代实际上是极端情况的策略迭代。

• 最优化原则

一个最优策略可以被分解为两部分：从状态 $s$ 到下一个状态 $s’$ 采取了最优行为；在状态 $s’$ 时遵循一个最优策略。

定理： 策略 $\pi(a\mid s)$ 能在状态 $s$ 获得最优价值，即 $V_\pi(s)=V_*(s)$，当且仅当，对于任意状态 $s$ 可以到达的状态 $s^\prime$ ，该策略在 $s^\prime$ 的价值是最优价值，即 $V_\pi(s^\prime)=V_*(s)$ 。

如果我们知道了子问题的最优解 $V_*(s^\prime)$ ，则 $V_*(s)$ 可以通过一步得到：

$$V_{*}(s) \leftarrow \max _{a \in \mathcal{A}} \mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} V_{*}\left(s^{\prime}\right)$$

价值迭代就是上述过程的迭代进行，可同步迭代，即对于第 $k+1$ 次迭代，所有的状态 $s$ 的价值 $V_{k+1}(s)$ 用 $V_k(s')$ 计算并更新，其中 $s’$ 是 $s$ 的上一状态。或异步迭代，状态更新单独进行。两种迭代方式均会收敛。

$$ \begin{aligned} V_{k+1}(s) &=\max _{a \in \mathcal{A}}\left(\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} V_{k}\left(s^{\prime}\right)\right) \\ \mathbf{V}_{k+1} &=\max _{a \in \mathcal{A}} \mathcal{R}^{\mathbf{a}}+\gamma \mathcal{P}^{\mathbf{a}} \mathbf{V}_{k} \end{aligned} $$

• 价值迭代收敛性证明

考虑价值函数上的向量空间 $\mathcal{V}$，显然它是 $\mid S\mid$ 维的，该空间中每一点都是一个价值函数 $V(s)$ (泛函)；

在该空间上定义范数度量，对于任意价值函数 $u$ 和 $v$ ，它们之间的距离定义为：

$$\mid \mid u-v\mid \mid_\infty=\max_{s\in S} \mid u(s)-v(s)\mid$$

由于 $(\mathcal{V},\mid\mid \cdot\mid\mid)$ 是有限维的赋范空间，必完备，故是巴拿赫空间。

定义价值迭代算子 $\mathcal{T}$：

$$\begin{aligned} V_{k+1}(s) &=\left[\mathcal{T}\left(V_{k}\right)\right](s) =\max _{a}\left(\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime}} \mathcal{P}_{s s^{\prime}}^{a} V_{k}\left(s^{\prime}\right)\right) \end{aligned}$$

此时，贝尔曼最优方程写为：

$$\begin{aligned} V_{*}(s) &=\left[\mathcal{T}\left(V_{*}\right)\right](s) =\max _{a}\left(\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime}} \mathcal{P}_{s s^{\prime}}^{a} V_{*}\left(s^{\prime}\right)\right) \end{aligned}$$

下证价值迭代算子为巴拿赫空间上的压缩算子。

证明：

$$\begin{array}{l} |[\mathcal{T}(u)](s)-[\mathcal{T}(v)](s)|, \quad \forall s \in \mathcal{S} \\ =\left|\max _{a_{1}}\left(\mathcal{R}^{a_{1}}+\gamma \sum_{s^{\prime}} \mathcal{P}_{s s^{\prime}}^{a_{1}} u\left(s^{\prime}\right)\right)-\max _{a_{2}}\left(\mathcal{R}^{a_{2}}+\gamma \sum_{s^{\prime}} \mathcal{P}_{s s^{\prime}}^{a_{2}} v\left(s^{\prime}\right)\right)\right| \\ \leq \max _{a}\left|\left(\mathcal{R}^{a}+\gamma \sum_{s^{\prime}} \mathcal{P}_{s s^{\prime}}^{a} u\left(s^{\prime}\right)\right)-\left(\mathcal{R}^{a}+\gamma \sum_{s^{\prime}} \mathcal{P}_{s s^{\prime}}^{a} v\left(s^{\prime}\right)\right)\right| \\ =\gamma \max _{a}\left|\sum_{s^{\prime}} \mathcal{P}_{s s^{\prime}}^{a}\left(u\left(s^{\prime}\right)-v\left(s^{\prime}\right)\right)\right| \\ \leq \gamma\|u-v\|_{\infty} \quad(\gamma<1) \end{array}$$

此即 $\|\mathcal{T}(u-v)\|_{\infty}<\|u-v\|_{\infty}$ ，故 $\mathcal{T}$ 为压缩算子。

由巴拿赫压缩不动点定理，算子 $\mathcal{T}$ 有唯一不动点，这恰就是最优价值 $V_*$ ，$V_k\rightarrow V_*$。

• 例子：在一个4*4的方格世界中，找到任一一个方格到最左上角方格的最短路径

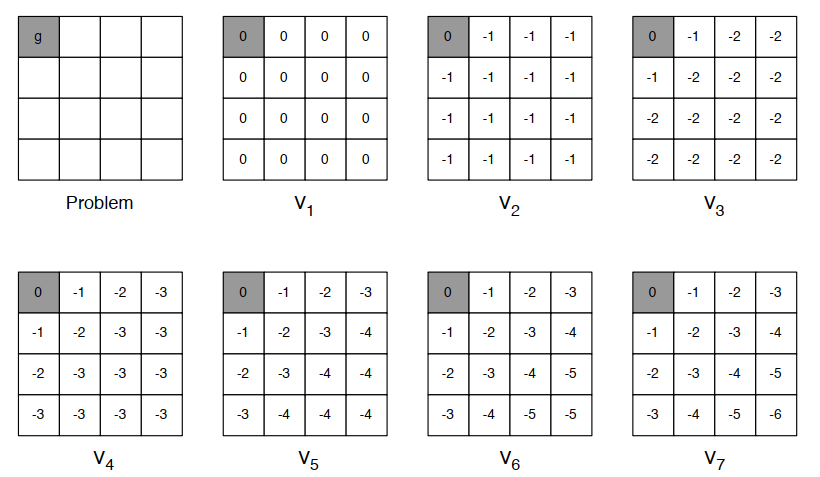
**方案1：**确定性价值迭代

简要思路：如果我们清楚地知道期望的最终状态的位置以及状态间关系，那么可以认为是一个确定性价值迭代**。**此时，可以把问题分解成一些列的子问题，从最终目标状态开始分析，逐渐往回推，直至推至所有状态。

上例中，在已知左上角为最终目标的情况下，可以从与左上角相邻的两个方格开始计算，因为这两个方格是可以仅通过 1 步就到达目标状态的状态，或者说目标状态是这两个状态的后继状态。最短路径可以量化为：每移动一步获得一个 -1 的即时奖励。为此我们可以更新与目标方格相邻的这两个方格的状态价值为 -1。如此依次向右下角倒推，直至所有状态找到最短路径。

**方案2：**一般价值迭代

并不确定最终状态在哪里，而是根据上一步迭代中每一个状态的最优状态价值来更新当前状态的最优状态价值。多次迭代最终也将收敛。

**注意：**与策略迭代不同，在价值迭代中，算法不会给出明确的策略，迭代过程中得到的价值函数，不对应任何策略。

扩展

• In-place 动态规划

即异步动态规划，直接原地更新下一个状态的v值，而不像同步迭代那样需要额外存储新的v值。在这种情况下，更新状态价值的顺序有时候会比较有意义。

• 重要状态优先更新

使用Bellman error：

$$\left|\max _{a \in \mathcal{A}}\left(\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} V\left(s^{\prime}\right)\right)-V(s)\right|$$

Bellman error 反映的是当前的状态价值与更新后的状态价值差的绝对值。Bellman error越大，越有必要优先更新，对那些Bellman error较大的状态进行存储。

• 采样更新

尽管动态规划一定程度上简化了问题的描述，但动态规划使用 full-width backups。在MDP 中，对于每一次状态更新，都要考虑到所有状态及所有可能的动作，同时还要使用 MDP 中的状态转移矩阵、奖励函数。DP 解决 MDP 问题的这一特点决定了其仅对中等规模(百万级别的状态数)的问题较为有效，对于更大规模的问题，会带来维度灾难。

通过蒙特卡洛采样更新可以打破维度灾难。

• 近似动态规划

使用其他技术手段(例如神经网络)建立一个参数较少，消耗计算资源较少、同时虽然不完全精确但却够用的近似价值函数。

Q.E.D.