介绍
第二三讲告诉了我们如何从理论上解决一个已知的 MDP 问题,利用贝尔曼方程,通过 DP 来评估一个给定的策略,接着贪婪选取动作,如此反复最终确定最优策略;也可以直接进行不基于任何策略的价值迭代得到最优价值函数和最优策略。
然而并非所有的 MDP 问题都掌握 MDP 的所有细节,本节的目的就是解决一个可以被认为是 MDP、但却不掌握 MDP 具体细节的问题,直接从 Agent 与环境的交互来得得到一个估计的最优价值函数和最优策略。这部分内容同样分为两部分,第一部分也就是本讲的内容,聚焦于策略评估,也就是 prediction,直白的说就是在给定的策略同时不清楚 MDP 细节的情况下,估计 Agent 会得到怎样的期望奖励。下一讲将利用本讲的主要思想解决 control 问题进而找出最优策略,最大化Agent 的奖励。
Monte-Carlo 策略评估
蒙特卡洛强化学习 :在不清楚MDP状态转移及即时奖励的情况下,直接从经历完整的轨迹来学习状态价值,通常情况下某状态的价值等于在多个轨迹中以该状态得到的所有回报的平均。
注:收获不是针对轨迹的,它存在于轨迹内,针对于轨迹中某一个状态,从这个状态开始经历完轨迹时得到的有衰减的奖励的总和。从一个轨迹中,我们可以得到该轨迹内所有状态的回报。当一个状态在轨迹内出现多次,该状态的收获有不同的计算方法,后面会讲到。
蒙特卡洛策略评估 Monte-Carlo Policy Evaluation :
**目标:**在给定策略下,从完整轨迹中学习该策略下的状态价值函数。
特点:(1) 无模型,不需要 MDP 的转移和奖励函数;(2) 根据完整的轨迹学习,无自举。使用 MC 方法通常要求轨迹要足够长且达到终止状态。
数学描述如下,基于特定策略 π \pi π
s 1 , a 1 , r 2 , s 2 , a 2 , ⋯ , s t , a t , r t + 1 , ⋯ , s k ∼ π s_1,a_1,r_2,s_2,a_2,\cdots,s_t,a_t,r_{t+1},\cdots,s_k\sim \pi
s 1 , a 1 , r 2 , s 2 , a 2 , ⋯ , s t , a t , r t + 1 , ⋯ , s k ∼ π
t t t s t s_t s t
G t = r t + 1 + γ r t + 2 + ⋯ + γ T − 1 r t + T G_{t}=r_{t+1}+\gamma r_{t+2}+\cdots+\gamma^{T-1} r_{t+T}
G t = r t + 1 + γ r t + 2 + ⋯ + γ T − 1 r t + T
价值则是回报的期望:
V π ( s ) = E π [ G t ∣ s t = s ] V_{\pi}(s)=\mathbb{E}_{\pi}[G_t|s_t=s]
V π ( s ) = E π [ G t ∣ s t = s ]
蒙特卡洛策略评估方法使用回报的经验均值作为回报的期望。在状态转移过程中,可能发生一个状态经过一定的转移后又一次或多次返回该状态,此时在轨迹里如何计算这个状态发生的次数和计算该轨迹的收获呢?可以有如下两种方法:
首次经过的 MC 策略评估
为了评估状态 s s s 首次 遇到状态 s s s t t t N ( s ) ← N ( s ) + 1 N(s) ← N(s) + 1 N ( s ) ← N ( s ) + 1 t t t S ( s ) ← S ( s ) + G t S(s) ← S(s) + G_t S ( s ) ← S ( s ) + G t N ( s ) → ∞ N(s) → ∞ N ( s ) → ∞
每次经过的 MC 策略评估
为了评估状态 s s s 每次 遇到状态 s s s t t t N ( s ) ← N ( s ) + 1 N(s) ← N(s) + 1 N ( s ) ← N ( s ) + 1 t t t S ( s ) ← S ( s ) + G t S(s) ← S(s) + G_t S ( s ) ← S ( s ) + G t N ( s ) → ∞ N(s) → ∞ N ( s ) → ∞
增量式更新均值 :
对一组不断产生新数据的序列 x 1 , x 2 , ⋯ , x k − 1 , x k x_1,x_2,\cdots,x_{k-1},x_k x 1 , x 2 , ⋯ , x k − 1 , x k μ 1 , μ 2 , \mu_1,\mu_2, μ 1 , μ 2 , ⋯ , u k − 1 , μ k \cdots,u_{k-1},\mu_k ⋯ , u k − 1 , μ k
μ k = 1 k ∑ j = 1 k x j = 1 k ( x k + ∑ j = 1 k − 1 x j ) = 1 k ( x k + ( k − 1 ) μ k − 1 ) = μ k − 1 + 1 k ( x k − μ k − 1 ) \begin{aligned}
\mu_{k} &=\frac{1}{k} \sum_{j=1}^{k} x_{j} \\
&=\frac{1}{k}\left(x_{k}+\sum_{j=1}^{k-1} x_{j}\right) \\
&=\frac{1}{k}\left(x_{k}+(k-1) \mu_{k-1}\right) \\
&=\mu_{k-1}+\frac{1}{k}\left(x_{k}-\mu_{k-1}\right)
\end{aligned}
μ k = k 1 j = 1 ∑ k x j = k 1 ( x k + j = 1 ∑ k − 1 x j ) = k 1 ( x k + ( k − 1 ) μ k − 1 ) = μ k − 1 + k 1 ( x k − μ k − 1 )
只需要记录前一时刻的均值和当前时刻的观测量。
把这个方法应用于蒙特卡洛策略评估,就得到增量式的 MC 更新。对于一系列片段中每一个 s 1 , a 1 , r 2 , s 2 , a 2 , ⋯ , s t , a t , t t + 1 , ⋯ , s k s_1,a_1,r_2,s_2,a_2,\cdots,s_t,a_t,t_{t+1},\cdots,s_k s 1 , a 1 , r 2 , s 2 , a 2 , ⋯ , s t , a t , t t + 1 , ⋯ , s k
N ( s t ) ← N ( s t ) + 1 V ( s t ) ← V ( s t ) + 1 N ( s t ) ( G t − V ( s t ) ) \begin{array}{l}
N\left(s_{t}\right) \leftarrow N\left(s_{t}\right)+1 \\
V\left(s_{t}\right) \leftarrow V\left(s_{t}\right)+\frac{1}{N\left(s_{t}\right)}\left(G_{t}-V\left(s_{t}\right)\right)
\end{array}
N ( s t ) ← N ( s t ) + 1 V ( s t ) ← V ( s t ) + N ( s t ) 1 ( G t − V ( s t ) )
随着状态遍历次数的增加,1 / N ( s t ) → 0 1/N(s_t)\rightarrow 0 1 / N ( s t ) → 0
如果环境是动态、不断变化的,更希望能够随时跟踪当前不断变化的均值,可用学习率更新:
V ( s t ) ← V ( s t ) + α ( G t − V ( s t ) ) V\left(s_{t}\right) \leftarrow V\left(s_{t}\right)+\alpha\left(G_{t}-V\left(s_{t}\right)\right)
V ( s t ) ← V ( s t ) + α ( G t − V ( s t ) )
其中 α \alpha α
时间差分学习 Temporal-Difference Learning
回顾策略价值定义和 MC 评估方法:
V π ( s t ) = E π [ G t ] , a k ∼ π ( s k ) V ( s t ) ← V ( s t ) + α ( G t − V ( s t ) ) \begin{aligned}
V_{\pi}\left(s_{t}\right)=\mathbb{E}_{\pi}\left[G_{t}\right], \quad a_{k} \sim \pi\left(s_{k}\right)\\
V\left(s_{t}\right) \leftarrow V\left(s_{t}\right)+\alpha\left(G_{t}-V\left(s_{t}\right)\right)
\end{aligned}
V π ( s t ) = E π [ G t ] , a k ∼ π ( s k ) V ( s t ) ← V ( s t ) + α ( G t − V ( s t ) )
策略价值的另一定义是贝尔曼期望方程,如果多观测一步来代替期望,这就引出了时间差分学习:
V π ( s t ) = E π [ r t + 1 + γ V π ( s t + 1 ) ] , a t ∼ π ( s t ) V ( s t ) ← V ( s t ) + α ( r t + 1 + γ V π ( s t + 1 ) − V ( s t ) ) V_{\pi}\left(s_{t}\right)=\mathbb{E}_{\pi}\left[r_{t+1}+\gamma V_{\pi}\left(s_{t+1}\right)\right], \quad a_{t} \sim \pi\left(s_{t}\right)
\\
V\left(s_{t}\right) \leftarrow V\left(s_{t}\right)+\alpha\left(r_{t+1}+\gamma V_{\pi}\left(s_{t+1}\right)-V\left(s_{t}\right)\right)
V π ( s t ) = E π [ r t + 1 + γ V π ( s t + 1 ) ] , a t ∼ π ( s t ) V ( s t ) ← V ( s t ) + α ( r t + 1 + γ V π ( s t + 1 ) − V ( s t ) )
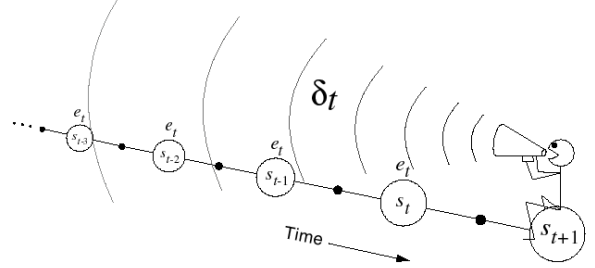
时间差分学习简称 TD 学习,它和蒙特卡洛学习一样,它也从 Episode 学习,是 model-free 的;但是它可以学习不完整 的 Episode,通过自举(bootstrapping) 猜测 Episode 的结果,并持续更新这个猜测。
上式中 r t + 1 + γ V π ( s t + 1 ) r_{t+1}+\gamma V_{\pi}\left(s_{t+1}\right) r t + 1 + γ V π ( s t + 1 ) δ t = r t + 1 + γ V π ( s t + 1 ) − V ( s t ) \delta_t=r_{t+1}+\gamma V_{\pi}\left(s_{t+1}\right)-V(s_t) δ t = r t + 1 + γ V π ( s t + 1 ) − V ( s t ) 自举 (bootstrapping) 指的就是用 TD 目标值代替回报 G t G_t G t
MC 和 TD评估的基本区别 :例如,你想获得开车去公司的时间,每天上班开车的经历就是一次采样。假设今天在路口 A 遇到了堵车,
TD 会在路口 A 就开始更新预计到达路口 B、路口 C ⋯ ⋯ \cdots \cdots ⋯ ⋯
而 MC 并不会立即更新时间,而是在每次到达公司后,再修改到达每个路口和公司的时间。
TD 可以在智能体运行过程中的每一时刻在线更新,MC 需要完整的轨迹计算出回报后更新,TD 可以根据不完整的轨迹学习,MC 要求轨迹达到终止状态或序列足够长。
MC 与 TD 偏差方差权衡 :
回报 G t = r t + 1 + γ r t + 2 + ⋯ + γ T − 1 r t G_{t}=r_{t+1}+\gamma r_{t+2}+\cdots+\gamma^{T-1} r_{t} G t = r t + 1 + γ r t + 2 + ⋯ + γ T − 1 r t V π ( s t ) V_{\pi}\left(s_{t}\right) V π ( s t ) V π ( s t ) = E π [ G t ] V_{\pi}\left(s_{t}\right)=\mathbb{E}_{\pi}\left[G_{t}\right] V π ( s t ) = E π [ G t ] r t + 1 + γ V π ( s t + 1 ) r_{t+1}+\gamma V_{\pi}\left(s_{t+1}\right) r t + 1 + γ V π ( s t + 1 ) V π ( s t ) V_{\pi}\left(s_{t}\right) V π ( s t ) V π ( s t ) = E π [ r t + 1 + γ V π ( s t + 1 ) ] V_{\pi}\left(s_{t}\right)=\mathbb{E}_{\pi}\left[r_{t+1}+\gamma V_{\pi}\left(s_{t+1}\right)\right] V π ( s t ) = E π [ r t + 1 + γ V π ( s t + 1 ) ] r t + 1 + γ V ( s t + 1 ) r_{t+1}+\gamma V\left(s_{t+1}\right) r t + 1 + γ V ( s t + 1 ) V π ( s t ) V_{\pi}\left(s_{t}\right) V π ( s t ) G t G_t G t
因此,MC 是 高方差, 零偏差,有好的收敛性(即使是使用逼近器也能保证收敛),与价值函数初始值无关,原理简单,使用方便;TD 是低方差,有偏差,通常情况是比 MC 更有效,TD(0) 能够收敛到 V π ( s ) V_π(s) V π ( s )
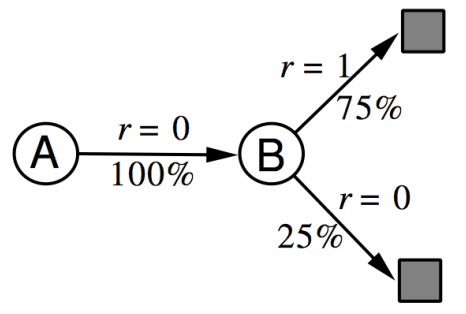
例子 :求 A, B 的状态价值
解:对于 MC 方法,由于需要完整的片段,因此仅片段 1 可以用于计算 V ( A ) = 0 / 8 = 0 V(A)=0/8=0 V ( A ) = 0 / 8 = 0 V ( B ) = 6 / 8 V(B)=6/8 V ( B ) = 6 / 8 V ( A ) = V ( B ) = 6 / 8 V(A)=V(B)=6/8 V ( A ) = V ( B ) = 6 / 8
MC 收敛结果对应最小二乘误差,最佳匹配观测 ( s t , G t ) \left(s_{t}, G_{t}\right) ( s t , G t )
∑ k = 1 K ∑ t = 1 T k ( G t k − V ( s t k ) ) 2 \sum_{k=1}^{K} \sum_{t=1}^{T_{k}}\left(G_{t}^{k}-V\left(s_{t}^{k}\right)\right)^{2}
k = 1 ∑ K t = 1 ∑ T k ( G t k − V ( s t k ) ) 2
TD(0) 收敛结果对应最大似然马尔可夫模型,TD 会为已观测到的信息建立一个最佳匹配观测数据 ( s t , a t , r t + 1 , s t + 1 ) \left(s_{t}, a_{t}, r_{t+1}, s_{t+1}\right) ( s t , a t , r t + 1 , s t + 1 ) ⟨ S , A , P ^ , R ^ , γ ⟩ \langle\mathcal{S}, \mathcal{A}, \hat{\mathcal{P}}, \hat{\mathcal{R}}, \gamma\rangle ⟨ S , A , P ^ , R ^ , γ ⟩
P ^ s , s ′ a = 1 N ( s , a ) ∑ k = 1 K ∑ t = 1 T k I ( s t k , a t k , s t + 1 k = s , a , s ′ ) R ^ s a = 1 N ( s , a ) ∑ k = 1 K ∑ t = 1 T k I ( s t k , a t k = s , a ) r t k \begin{aligned}
\hat{\mathcal{P}}_{s, s^{\prime}}^{a} &=\frac{1}{N(s, a)} \sum_{k=1}^{K} \sum_{t=1}^{T_{k}} \mathcal{I}\left(s_{t}^{k}, a_{t}^{k}, s_{t+1}^{k}=s, a, s^{\prime}\right) \\
\hat{\mathcal{R}}_{s}^{a} &=\frac{1}{N(s, a)} \sum_{k=1}^{K} \sum_{t=1}^{T_{k}} \mathcal{I}\left(s_{t}^{k}, a_{t}^{k}=s, a\right) r_{t}^{k}
\end{aligned}
P ^ s , s ′ a R ^ s a = N ( s , a ) 1 k = 1 ∑ K t = 1 ∑ T k I ( s t k , a t k , s t + 1 k = s , a , s ′ ) = N ( s , a ) 1 k = 1 ∑ K t = 1 ∑ T k I ( s t k , a t k = s , a ) r t k
因此,TD 能够利用马尔可夫性,在一个马尔可夫环境下会更有效;MC 不能利用马尔可夫性。
三种 RL 算法的对比
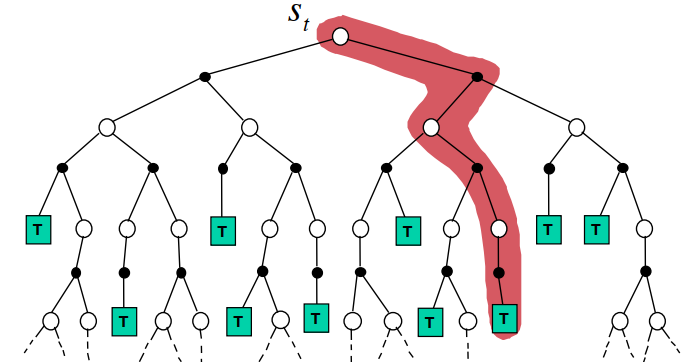
MC:一次完整经历,用实际收获更新状态预估价值
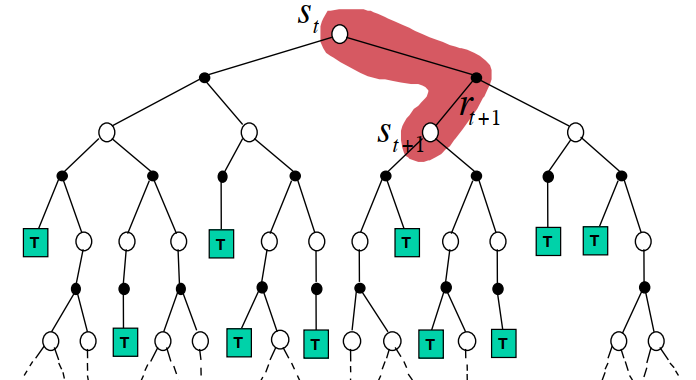
TD:采样,经历可不完整,可用自举更新预估价值
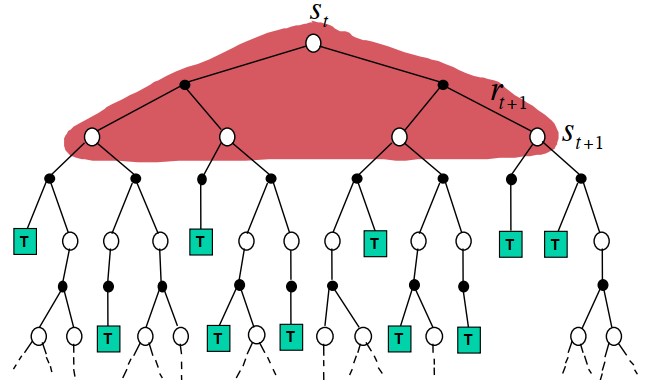
DP:没有采样,根据完整模型更新状态价值
对比:
TD(λ \lambda λ
先前所介绍的 TD 算法实际上都是 TD(0) 算法,表示在当前状态下往前多看1步 G t ( 1 ) = r t + 1 + γ V ( s t + 1 ) G_t^{(1)}=r_{t+1}+\gamma V(s_{t+1}) G t ( 1 ) = r t + 1 + γ V ( s t + 1 ) G t = r t + 1 + γ r t + 2 + ⋯ G_t=r_{t+1}+\gamma r_{t+2}+\cdots G t = r t + 1 + γ r t + 2 + ⋯
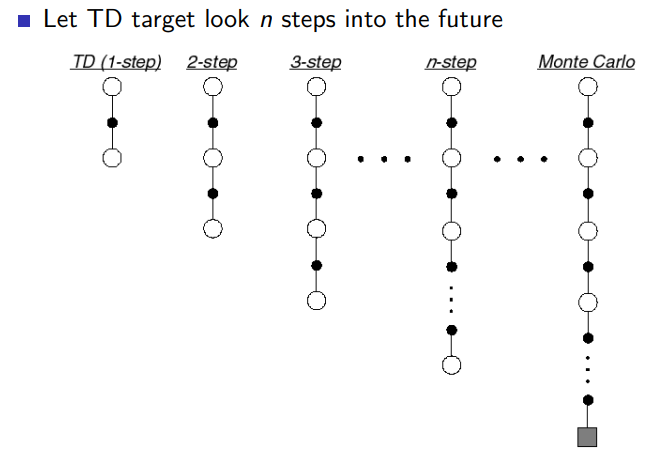
n-步回报 :
n = 1 ( T D ) G t ( 1 ) = r t + 1 + γ V ( s t + 1 ) n = 2 G t ( 2 ) = r t + 1 + γ r t + 2 + γ 2 V ( s t + 2 ) ⋮ n = ∞ ( MC) G t ( ∞ ) = r t + 1 + γ r t + 2 + ⋯ + γ t + T − 1 r T \begin{array}{lll}
n=1 & (T D) & G_{t}^{(1)}=r_{t+1}+\gamma V\left(s_{t+1}\right) \\
n=2 & & G_{t}^{(2)}=r_{t+1}+\gamma r_{t+2}+\gamma^{2} V\left(s_{t+2}\right) \\
\vdots & & \\
n=\infty & (\text { MC) } & G_{t}^{(\infty)}=r_{t+1}+\gamma r_{t+2}+\cdots+\gamma^{t+T-1} r_{T}
\end{array}
n = 1 n = 2 ⋮ n = ∞ ( T D ) ( MC) G t ( 1 ) = r t + 1 + γ V ( s t + 1 ) G t ( 2 ) = r t + 1 + γ r t + 2 + γ 2 V ( s t + 2 ) G t ( ∞ ) = r t + 1 + γ r t + 2 + ⋯ + γ t + T − 1 r T
定义n-步回报:
G t ( n ) = r t + 1 + γ r t + 2 + ⋯ + γ n − 1 r t + n + γ n V ( s t + n ) G_{t}^{(n)}=r_{t+1}+\gamma r_{t+2}+\cdots+\gamma^{n-1} r_{t+n}+\gamma^{n} V\left(s_{t+n}\right)
G t ( n ) = r t + 1 + γ r t + 2 + ⋯ + γ n − 1 r t + n + γ n V ( s t + n )
于是得到 n-步时间差分学习方法:
V ( s t ) ← V ( s t ) + α ( G t ( n ) − V ( s t ) ) V\left(s_{t}\right) \leftarrow V\left(s_{t}\right)+\alpha\left(G_{t}^{(n)}-V\left(s_{t}\right)\right)
V ( s t ) ← V ( s t ) + α ( G t ( n ) − V ( s t ) )
n步回报的误差上届 :
1 步回报和真实 V π V_{\pi} V π
max s t ∣ E [ G t ( 1 ) ] − V π ( s t ) ∣ = max s t ∣ E [ r t + 1 + γ V ( s t + 1 ) ] − V π ( s t ) ∣ = max s t ∣ [ T π ( V ) ] ( s t ) − V π ( s t ) ∣ ≤ γ ∥ V − V π ∥ \begin{aligned}
\max _{s_{t}}\left|\mathbb{E}\left[G_{t}^{(1)}\right]-V_{\pi}\left(s_{t}\right)\right| &=\max _{s_{t}}\left|\mathbb{E}\left[r_{t+1}+\gamma V\left(s_{t+1}\right)\right]-V_{\pi}\left(s_{t}\right)\right| \\
&=\max _{s_{t}}\left|\left[\mathcal{T}^{\pi}(V)\right]\left(s_{t}\right)-V_{\pi}\left(s_{t}\right)\right| \\
& \leq \gamma\left\|V-V_{\pi}\right\|
\end{aligned}
s t max ∣ ∣ ∣ ∣ E [ G t ( 1 ) ] − V π ( s t ) ∣ ∣ ∣ ∣ = s t max ∣ E [ r t + 1 + γ V ( s t + 1 ) ] − V π ( s t ) ∣ = s t max ∣ [ T π ( V ) ] ( s t ) − V π ( s t ) ∣ ≤ γ ∥ V − V π ∥
其中 T π \mathcal{T}^{\pi} T π T π ( V ) = R π + γ P π V \mathcal{T}^{\pi}\left(V\right)=\mathcal{R}^{\pi}+\gamma \mathcal{P}^{\pi} V T π ( V ) = R π + γ P π V
max s t ∣ E [ G t ( n ) ] − V π ( s t ) ∣ = max s t ∣ E [ r t + 1 + γ r t + 1 + … γ n V ( s t + n ) ] − V π ( s t ) ∣ = max s t ∣ E [ r t + 1 + γ E [ r t + 2 + ⋯ + γ E [ r t + n + γ V ( s t + n ) ] … ] ] − V π ( s t ) ∣ = max s t ∣ T π ∘ ⋯ ∘ T π ⏟ n ( V ) ] ( s t ) − V π ( s t ) ∣ ≤ γ n ∥ V − V π ∥ \begin{aligned}
& \max _{s_{t}}\left|\mathbb{E}\left[G_{t}^{(n)}\right]-V_{\pi}\left(s_{t}\right)\right| \\
=& \max _{s_{t}}\left|\mathbb{E}\left[r_{t+1}+\gamma r_{t+1}+\ldots \gamma^{n} V\left(s_{t+n}\right)\right]-V_{\pi}\left(s_{t}\right)\right| \\
=& \max _{s_{t}}\left|\mathbb{E}\left[r_{t+1}+\gamma \mathbb{E}\left[r_{t+2}+\cdots+\gamma \mathbb{E}\left[r_{t+n}+\gamma V\left(s_{t+n}\right)\right] \ldots\right]\right]-V_{\pi}\left(s_{t}\right)\right| \\
=&\max _{s_{t}} \mid \underbrace{\mathcal{T}^{\pi} \circ \cdots \circ \mathcal{T}^{\pi}}_{n}(V)]\left(s_{t}\right)-V_{\pi}\left(s_{t}\right) \mid \\
\leq & \gamma^{n}\left\|V-V_{\pi}\right\|
\end{aligned}
= = = ≤ s t max ∣ ∣ ∣ ∣ E [ G t ( n ) ] − V π ( s t ) ∣ ∣ ∣ ∣ s t max ∣ E [ r t + 1 + γ r t + 1 + … γ n V ( s t + n ) ] − V π ( s t ) ∣ s t max ∣ E [ r t + 1 + γ E [ r t + 2 + ⋯ + γ E [ r t + n + γ V ( s t + n ) ] … ] ] − V π ( s t ) ∣ s t max ∣ n T π ∘ ⋯ ∘ T π ( V ) ] ( s t ) − V π ( s t ) ∣ γ n ∥ V − V π ∥
n-步回报对应更准确的价值估计,n 越大,估计和真实价值之间的误差上界越低,但是估计的方差会变大。为了平衡偏差和方差,通常将不同步回报进行加权,如 G ← 1 2 G ( 2 ) + 1 2 G ( 4 ) G\leftarrow \frac{1}{2}G^{(2)}+\frac{1}{2}G^{(4)} G ← 2 1 G ( 2 ) + 2 1 G ( 4 ) λ \lambda λ
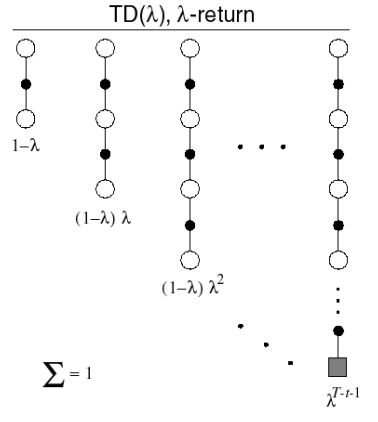
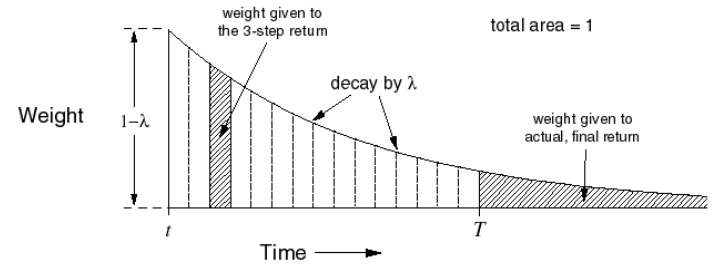
λ \lambda λ G t λ G_{t}^{\lambda} G t λ G t ( n ) G_{t}^{(n)} G t ( n ) 0 < λ < 1 0<\lambda<1 0 < λ < 1 ( 1 − λ ) λ n − 1 (1-\lambda) \lambda^{n-1} ( 1 − λ ) λ n − 1
G t λ = ( 1 − λ ) ∑ n = 1 ∞ λ n − 1 G t ( n ) G_{t}^{\lambda}=(1-\lambda) \sum_{n=1}^{\infty} \lambda^{n-1} G_{t}^{(n)}
G t λ = ( 1 − λ ) n = 1 ∑ ∞ λ n − 1 G t ( n )
前向更新的 T D ( λ ) \mathrm{TD}(\lambda) T D ( λ )
V ( s t ) ← V ( s t ) + α ( G t λ − V ( s t ) ) V\left(s_{t}\right) \leftarrow V\left(s_{t}\right)+\alpha\left(G_{t}^{\lambda}-V\left(s_{t}\right)\right)
V ( s t ) ← V ( s t ) + α ( G t λ − V ( s t ) )
从公式中可以看到,对于 n n n G t ( n ) G_t^{(n)} G t ( n ) 既利用了长步数估计的精度,又降低了高方差的影响。
前向 TD( λ ) (\lambda) ( λ ) :
V ( s t ) ← V ( s t ) + α ( G t λ − V ( s t ) ) V\left(s_{t}\right) \leftarrow V\left(s_{t}\right)+\alpha\left(G_{t}^{\lambda}-V\left(s_{t}\right)\right)
V ( s t ) ← V ( s t ) + α ( G t λ − V ( s t ) )
这样的更新计算中,为了更新价值函数向 λ λ λ G t ( n ) G^{(n)}_t G t ( n ) S S S
注:这里的离线学习举个例子就是打游戏只有每次通关后才复盘改进;而在线学习是边玩边学。
后向TD( λ ) (\lambda) ( λ )
对于事件发生的结果,可以有两种解释,频率启发 Frequency heuristic:将原因归因于出现频率最高的状态;就近启发 Recency heuristic:将原因归因于较近的几次状态。于是可以给每个状态引入一个数值:资格迹 ,它结合了两种启发。
资格迹 :对有限 MDP 问题,会为每个状态定义一个资格迹 E 0 ( s ) = 0 , ∀ s ∈ S E_{0}(s)=0, \forall s \in \mathcal{S} E 0 ( s ) = 0 , ∀ s ∈ S γ λ \gamma \lambda γ λ
E t ( S ) = { γ λ E t − 1 ( S ) if S ≠ s t γ λ E t − 1 ( S ) + 1 if S = s t = γ λ E t − 1 ( S ) + I ( S = s s t ) \begin{aligned}
E_{t}(S) &=\left\{\begin{array}{ll}
\gamma \lambda E_{t-1}(S) & \text { if } S \neq s_{t} \\
\gamma \lambda E_{t-1}(S)+1 & \text { if } S=s_{t}
\end{array}\right.\\
&=\gamma \lambda E_{t-1}(S)+\mathcal{I}\left(S=s s_{t}\right)
\end{aligned}
E t ( S ) = { γ λ E t − 1 ( S ) γ λ E t − 1 ( S ) + 1 if S = s t if S = s t = γ λ E t − 1 ( S ) + I ( S = s s t )
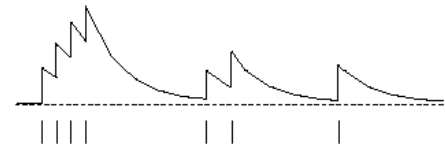
资格迹反映了被观测的次数和频率。
该图横坐标是时间,横坐标下有竖线的位置代表当前进入了状态 s s s E E E
δ t = r t + 1 + γ V π ( s t + 1 ) − V ( s t ) \delta_t=r_{t+1}+\gamma V_{\pi}\left(s_{t+1}\right)-V(s_t)
δ t = r t + 1 + γ V π ( s t + 1 ) − V ( s t )
所有状态的价值变化量等于 TD 误差乘上相应的资格迹:
V ( s t ) ← V ( s t ) + α δ t E t ( s ) , ∀ s ∈ S V\left(s_{t}\right) \leftarrow V\left(s_{t}\right)+\alpha\delta_tE_t(s),\quad \forall s\in S
V ( s t ) ← V ( s t ) + α δ t E t ( s ) , ∀ s ∈ S
后向 TD(λ λ λ
当 λ = 0 \lambda=0 λ = 0 TD ( λ ) \operatorname{TD}(\lambda) T D ( λ )
E t ( s ) = { 0 if s ≠ s t 1 if s = s t Δ V t ( s ) = { 0 if s ≠ s t α ⋅ δ t ⋅ 1 if s = s t \begin{array}{c}
E_{t}(s)=\left\{\begin{array}{ll}
0 & \text { if } s \neq s_{t} \\
1 & \text { if } s=s_{t}
\end{array}\right. \\
\Delta V_{t}(s)=\left\{\begin{array}{ll}
0 & \text { if } s \neq s_{t} \\
\alpha \cdot \delta_{t} \cdot 1 & \text { if } s=s_{t}
\end{array}\right.
\end{array}
E t ( s ) = { 0 1 if s = s t if s = s t Δ V t ( s ) = { 0 α ⋅ δ t ⋅ 1 if s = s t if s = s t
等同于前面介绍的 TD(0) 方法
V ( s t ) ← V ( s t ) + α δ t V\left(s_{t}\right) \leftarrow V\left(s_{t}\right)+\alpha \delta_{t}
V ( s t ) ← V ( s t ) + α δ t
考虑在一次轨迹中 S S S k k k λ = 1 \lambda=1 λ = 1
E t ( S ) = γ E t − 1 ( S ) + I ( S = s t ) = { 0 if t < k γ t − k if t ≥ k \begin{aligned}
E_{t}(S) &=\gamma E_{t-1}(S)+\mathcal{I}\left(S=s_{t}\right) \\
&=\left\{\begin{array}{ll}
0 & \text { if } t<k \\
\gamma^{t-k} & \text { if } t \geq k
\end{array}\right.
\end{aligned}
E t ( S ) = γ E t − 1 ( S ) + I ( S = s t ) = { 0 γ t − k if t < k if t ≥ k
于是 TD(1) 在整条轨迹上对 s s s
∑ t = 0 T α δ t E t ( s ) = α ∑ t = k T γ t − k δ t = δ k + γ δ k + 1 + γ 2 δ k + 2 + ⋯ + γ T − k δ T \begin{aligned}
\sum_{t=0}^{T} \alpha \delta_{t} E_{t}(s) &=\alpha \sum_{t=k}^{T} \gamma^{t-k} \delta_{t} \\
&=\delta_{k}+\gamma \delta_{k+1}+\gamma^{2} \delta_{k+2}+\cdots+\gamma^{T-k} \delta_{T}
\end{aligned}
t = 0 ∑ T α δ t E t ( s ) = α t = k ∑ T γ t − k δ t = δ k + γ δ k + 1 + γ 2 δ k + 2 + ⋯ + γ T − k δ T
假定 TD(1) 只在轨迹结束后对 V V V V V V
δ k + γ δ k + 1 + γ 2 δ k + 2 + ⋯ + γ T − k δ T = r k + 1 + γ V ( s k + 1 ) − V ( s k ) + γ r k + 2 + γ 2 V ( s k + 2 ) − γ V ( s k + 1 ) + γ 2 r k + 3 + γ 3 V ( s k + 3 ) − γ 2 V ( s k + 2 ) ⋮ + γ T − k r T + 1 − γ T − k V ( S T ) = r k + 1 + γ r k + 2 + γ 2 r k + 3 + ⋯ + γ T − k r T + 1 − V ( S k ) = G k − V ( s k ) \begin{aligned}
& \delta_{k}+\gamma \delta_{k+1}+\gamma^{2} \delta_{k+2}+\cdots+\gamma^{T-k} \delta_{T} \\
=& r_{k+1}+\gamma V\left(s_{k+1}\right)-V\left(s_{k}\right) \\
&+\gamma r_{k+2}+\gamma^{2} V\left(s_{k+2}\right)-\gamma V\left(s_{k+1}\right) \\
&+\gamma^{2} r_{k+3}+\gamma^{3} V\left(s_{k+3}\right)-\gamma^{2} V\left(s_{k+2}\right) \\
& \vdots \\
&+\gamma^{T-k} r_{T+1}-\gamma^{T-k} V\left(S_{T}\right) \\
=& r_{k+1}+\gamma r_{k+2}+\gamma^{2} r_{k+3}+\cdots+\gamma^{T-k} r_{T+1}-V\left(S_{k}\right) \\
=& G_{k}-V\left(s_{k}\right)
\end{aligned}
= = = δ k + γ δ k + 1 + γ 2 δ k + 2 + ⋯ + γ T − k δ T r k + 1 + γ V ( s k + 1 ) − V ( s k ) + γ r k + 2 + γ 2 V ( s k + 2 ) − γ V ( s k + 1 ) + γ 2 r k + 3 + γ 3 V ( s k + 3 ) − γ 2 V ( s k + 2 ) ⋮ + γ T − k r T + 1 − γ T − k V ( S T ) r k + 1 + γ r k + 2 + γ 2 r k + 3 + ⋯ + γ T − k r T + 1 − V ( S k ) G k − V ( s k )
因此离线 TD(1) 方法在同一条轨迹对某一状态的累计更新量等于对该状态的 MC 更新:
∑ t = 0 T α δ t E t ( s ) = α ( G k − V ( s k ) ) \sum_{t=0}^{T} \alpha \delta_{t} E_{t}(s)=\alpha(G_k-V(s_k))
t = 0 ∑ T α δ t E t ( s ) = α ( G k − V ( s k ) )
不过实际中往往使用在线 TD(1) ,因为在线更新效率更高,无需完整轨迹。
Q.E.D.