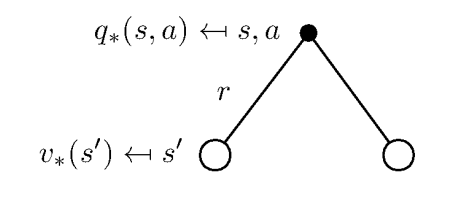马尔可夫决策过程(Markov Decision Process, MDP)
在强化学习中,马尔科夫决策过程(MDP)是对完全可观测的环境进行描述的,也就是说观测到的状态内容完整地决定了决策的需要的特征。几乎所有的强化学习问题都可以转化为MDP。
马尔可夫过程(Markov Process, MP)
如果一个状态的下一个状态只取决于当前所处状态,则称该状态转移具有马尔可夫性。设状态的历史为 h t = { s 1 , s 2 , s 3 , … , s t } h_{t}=\left\{s_{1}, s_{2}, s_{3}, \ldots, s_{t}\right\} h t = { s 1 , s 2 , s 3 , … , s t } h t h_t h t
P ( s t + 1 ∣ s t ) = P ( s t + 1 ∣ h t ) \mathbb{P}\left(s_{t+1} \mid s_{t}\right) =\mathbb{P}\left(s_{t+1} \mid h_{t}\right)
P ( s t + 1 ∣ s t ) = P ( s t + 1 ∣ h t )
P ( s t + 1 ∣ s t , a t ) = P ( s t + 1 ∣ h t , a t ) \mathbb{P}\left(s_{t+1} \mid s_{t}, a_{t}\right) =\mathbb{P}\left(s_{t+1} \mid h_{t}, a_{t}\right)
P ( s t + 1 ∣ s t , a t ) = P ( s t + 1 ∣ h t , a t )
马尔可夫性质是马尔可夫随机过程的基础。
也叫马尔科夫链(Markov Chain),它是一个无记忆的随机过程,可以用一个元组< S , P > <S,\mathcal{P}> < S , P > S S S P \mathcal{P} P
用状态转移矩阵来描述状态转移 P s s ′ = P ( s t + 1 = s ′ ∣ s t = s ) \mathcal{P}_{ss^\prime}=\mathbb{P}\left(s_{t+1}=s^{\prime} \mid s_{t}=s\right) P s s ′ = P ( s t + 1 = s ′ ∣ s t = s )
P = [ P ( s 1 ∣ s 1 ) P ( s 2 ∣ s 1 ) … P ( s n ∣ s 1 ) P ( s 1 ∣ s 2 ) P ( s 2 ∣ s 2 ) … P ( s n ∣ s 2 ) ⋮ ⋮ ⋱ ⋮ P ( s 1 ∣ s n ) P ( s 2 ∣ s n ) … P ( s n ∣ s n ) ] \mathcal{P}=\left[\begin{array}{cccc}
P\left(s_{1} \mid s_{1}\right) & P\left(s_{2} \mid s_{1}\right) & \ldots & P\left(s_{n} \mid s_{1}\right) \\
P\left(s_{1} \mid s_{2}\right) & P\left(s_{2} \mid s_{2}\right) & \ldots & P\left(s_{n} \mid s_{2}\right) \\
\vdots & \vdots & \ddots & \vdots \\
P\left(s_{1} \mid s_{n}\right) & P\left(s_{2} \mid s_{n}\right) & \ldots & P\left(s_{n} \mid s_{n}\right)
\end{array}\right]
P = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ P ( s 1 ∣ s 1 ) P ( s 1 ∣ s 2 ) ⋮ P ( s 1 ∣ s n ) P ( s 2 ∣ s 1 ) P ( s 2 ∣ s 2 ) ⋮ P ( s 2 ∣ s n ) … … ⋱ … P ( s n ∣ s 1 ) P ( s n ∣ s 2 ) ⋮ P ( s n ∣ s n ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
其中 n n n 1 1 1 ∑ i P ∗ i = 1 \sum_iP_{*i}=1 ∑ i P ∗ i = 1
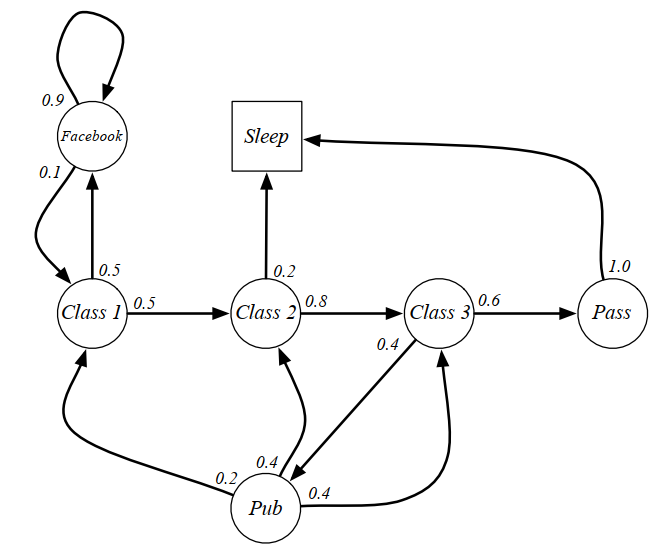
图中,圆圈表示学生所处的状态,方格Sleep是一个终止状态,或者可以描述成自循环的状态,也就是Sleep状态的下一个状态100%的几率还是自己。箭头表示状态之间的转移,箭头上的数字表示状态转移的概率。
举例说明:当学生处在第一节课(Class1)时,他有50%的几率会参加第2节课(Class2);同时也有50%的几率不在认真听课,进入到浏览facebook这个状态中。在浏览facebook这个状态时,他有90%的几率在下一时刻继续浏览,也有10%的几率返回到课堂内容上来。当学生进入到第二节课(Class2)时,会有80%的几率继续参加第三节课(Class3),也有20%的几率觉得课程较难而退出(Sleep)。当学生处于第三节课这个状态时,他有60%的几率通过考试,继而100%的退出该课程,也有40%的可能性需要到去图书馆之类寻找参考文献,此后根据其对课堂内容的理解程度,又分别有20%、40%、40%的几率返回值第一、二、三节课重新继续学习。一个可能的学生马尔科夫链从状态Class1开始,最终结束于Sleep,其间的过程根据状态转化图可以有很多种可能性,这些都称为Sample Episodes 。以下四个Episodes都是可能的:
C1 - C2 - C3 - Pass - Sleep
C1 - FB - FB - C1 - C2 - Sleep
C1 - C2 - C3 - Pub - C2 - C3 - Pass - Sleep
C1 - FB - FB - C1 - C2 - C3 - Pub - C1 - FB - FB - FB - C1 - C2 - C3 - Pub - C2 - Sleep
该学生马尔科夫过程的状态转移矩阵如下图:
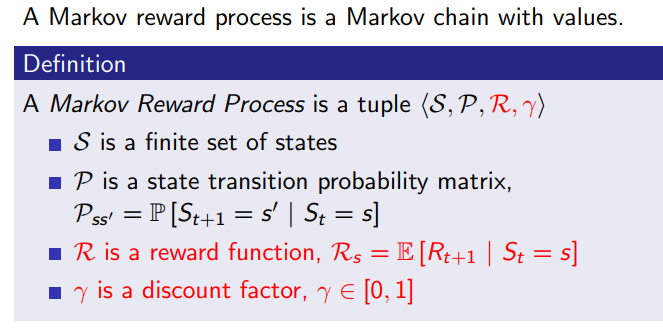
马尔可夫奖励过程(Markov Reward Process, MRP)
马尔科夫奖励过程在马尔科夫过程的基础上增加了奖励 R R R γ \gamma γ
注:为什么奖励是 t+1 时刻的?David 指出这仅是一个约定,为了在描述 RL 问题中涉及到的观测 O O O A A A R R R t t t s s s
衰减系数 Discount Factor :γ ∈ [ 0 , 1 ] \gamma\in [0,1] γ ∈ [ 0 , 1 ]
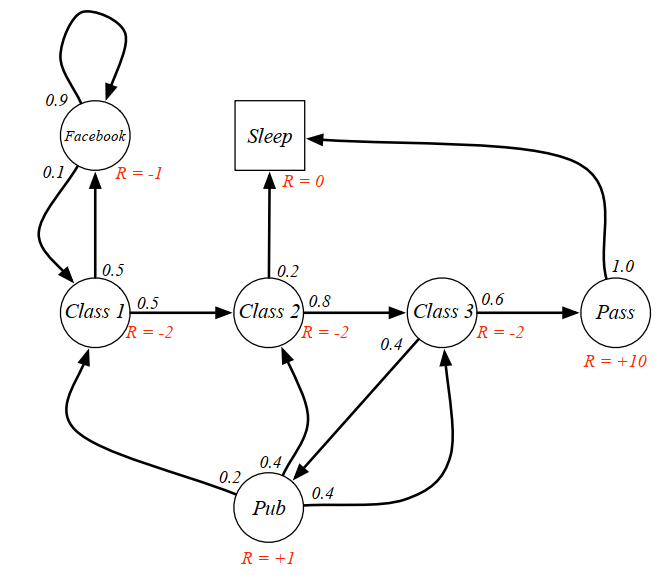
下图是一个 MRP 过程图示的例子,在 MP 过程基础上增加了针对每一个状态的奖励:
回报(return) :回报 G t G_t G t t t t
G t = r t + 1 + γ r t + 2 + γ 2 r t + 3 + γ 3 r t + 4 + … G_{t}=r_{t+1}+\gamma r_{t+2}+\gamma^{2} r_{t+3}+\gamma^{3} r_{t+4}+\ldots
G t = r t + 1 + γ r t + 2 + γ 2 r t + 3 + γ 3 r t + 4 + …
γ \gamma γ γ \gamma γ
回报对应某一具体的轨迹的收益,而状态价值代表所有轨迹的期望。
贝尔曼方程(Bellman Equation)
从价值函数里面可推导出贝尔曼方程,如下式所示:
V ( s ) = R ( s ) ⏟ Immediate reward + γ ∑ s ′ ∈ S P ( s ′ ∣ s ) V ( s ′ ) ⏟ Discounted sum of future reward V(s)=\underbrace{R(s)}_{\text {Immediate reward }}+\underbrace{\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s\right) V\left(s^{\prime}\right)}_{\text {Discounted sum of future reward }}
V ( s ) = Immediate reward R ( s ) + Discounted sum of future reward γ s ′ ∈ S ∑ P ( s ′ ∣ s ) V ( s ′ )
下面来证明贝尔曼方程,为此首先来证明如下式子(回报的期望等于回报的期望的期望。):
E [ V ( s t + 1 ) ∣ s t ] = E [ E [ G t + 1 ∣ s t + 1 ] ∣ s t ] = E [ G t + 1 ∣ s t ] \mathbb{E}[V(s_{t+1})|s_t]=\mathbb{E}[\mathbb{E}[G_{t+1}|s_{t+1}]|s_t]=E[G_{t+1}|s_t]
E [ V ( s t + 1 ) ∣ s t ] = E [ E [ G t + 1 ∣ s t + 1 ] ∣ s t ] = E [ G t + 1 ∣ s t ]
证明:简单起见,丢掉下标,令 s = s t , g ′ = G t + 1 , s ′ = s t + 1 s=s_t,g'=G_{t+1},s'=s_{t+1} s = s t , g ′ = G t + 1 , s ′ = s t + 1
E [ G t + 1 ∣ s t + 1 ] = E [ g ′ ∣ s ′ ] = ∑ g ′ g ′ p ( g ′ ∣ s ′ ) \mathbb{E}\left[G_{t+1} \mid s_{t+1}\right] =\mathbb{E}\left[g^{\prime} \mid s^{\prime}\right]
=\sum_{g^{\prime}} g^{\prime}~p\left(g^{\prime} \mid s^{\prime}\right)
E [ G t + 1 ∣ s t + 1 ] = E [ g ′ ∣ s ′ ] = g ′ ∑ g ′ p ( g ′ ∣ s ′ )
接着:
E [ E [ G t + 1 ∣ s t + 1 ] ∣ s t ] = E [ E [ g ′ ∣ s ′ ] ∣ s ] = ∑ s ′ ∑ g ′ g ′ p ( g ′ ∣ s ′ , s ) p ( s ′ ∣ s ) = ∑ s ′ ∑ g ′ g ′ p ( g ′ ∣ s ′ , s ) p ( s ′ ∣ s ) p ( s ) p ( s ) = ∑ s ′ ∑ g ′ g ′ p ( g ′ ∣ s ′ , s ) p ( s ′ , s ) p ( s ) = ∑ s ′ ∑ g ′ g ′ p ( g ′ , s ′ , s ) p ( s ) = ∑ s ′ ∑ g ′ g ′ p ( g ′ , s ′ ∣ s ) = ∑ g ′ ∑ s ′ g ′ p ( g ′ , s ′ ∣ s ) = ∑ g ′ g ′ p ( g ′ ∣ s ) = E [ g ′ ∣ s ] = E [ G t + 1 ∣ s t ] \begin{aligned}
\mathbb{E}\left[\mathbb{E}\left[G_{t+1} \mid s_{t+1}\right] \mid s_{t}\right] &=\mathbb{E} \left[\mathbb{E}\left[g^{\prime} \mid s^{\prime}\right] \mid s\right] \\
&=\sum_{s^{\prime}} \sum_{g^{\prime}} g^{\prime} p\left(g^{\prime} \mid s^{\prime}, s\right) p\left(s^{\prime} \mid s\right) \\
&=\sum_{s^{\prime}} \sum_{g^{\prime}} \frac{g^{\prime} p\left(g^{\prime} \mid s^{\prime}, s\right) p\left(s^{\prime} \mid s\right) p(s)}{p(s)} \\
&=\sum_{s^{\prime}} \sum_{g^{\prime}} \frac{g^{\prime} p\left(g^{\prime} \mid s^{\prime}, s\right) p\left(s^{\prime}, s\right)}{p(s)} \\
&=\sum_{s^{\prime}} \sum_{g^{\prime}} \frac{g^{\prime} p\left(g^{\prime}, s^{\prime}, s\right)}{p(s)} \\
&=\sum_{s^{\prime}} \sum_{g^{\prime}} g^{\prime} p\left(g^{\prime}, s^{\prime} \mid s\right) \\
&=\sum_{g^{\prime}} \sum_{s^{\prime}} g^{\prime} p\left(g^{\prime}, s^{\prime} \mid s\right) \\
&=\sum_{g^{\prime}} g^{\prime} p\left(g^{\prime} \mid s\right) \\
&=\mathbb{E}\left[g^{\prime} \mid s\right]=\mathbb{E}\left[G_{t+1} \mid s_{t}\right]
\end{aligned}
E [ E [ G t + 1 ∣ s t + 1 ] ∣ s t ] = E [ E [ g ′ ∣ s ′ ] ∣ s ] = s ′ ∑ g ′ ∑ g ′ p ( g ′ ∣ s ′ , s ) p ( s ′ ∣ s ) = s ′ ∑ g ′ ∑ p ( s ) g ′ p ( g ′ ∣ s ′ , s ) p ( s ′ ∣ s ) p ( s ) = s ′ ∑ g ′ ∑ p ( s ) g ′ p ( g ′ ∣ s ′ , s ) p ( s ′ , s ) = s ′ ∑ g ′ ∑ p ( s ) g ′ p ( g ′ , s ′ , s ) = s ′ ∑ g ′ ∑ g ′ p ( g ′ , s ′ ∣ s ) = g ′ ∑ s ′ ∑ g ′ p ( g ′ , s ′ ∣ s ) = g ′ ∑ g ′ p ( g ′ ∣ s ) = E [ g ′ ∣ s ] = E [ G t + 1 ∣ s t ]
于是得到 Bellman equation :
V ( s ) = E [ G t ∣ s t = s ] = E [ r t + 1 + γ r t + 2 + γ 2 r t + 3 + … ∣ s t = s ] = E [ r t + 1 + γ ( r t + 2 + γ r t + 3 + … ) ∣ s t = s ] = E [ r t + 1 + γ G t + 1 ∣ s t = s ] = E [ r t + 1 ∣ s t = s ] + γ E [ G t + 1 ∣ s t = s ] = R ( s ) + γ E [ G t + 1 ∣ s t = s ] = R ( s ) + γ E [ V ( s t + 1 ) ∣ s t = s ] = R ( s ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s ) V ( s ′ ) \begin{aligned}
V(s)&=\mathbb{E}\left[G_{t} \mid s_{t}=s\right]\\
&=\mathbb{E}\left[r_{t+1}+\gamma r_{t+2}+\gamma^{2} r_{t+3}+\ldots \mid s_{t}=s\right] \\
&=\mathbb{E}\left[r_{t+1}+\gamma (r_{t+2}+\gamma r_{t+3}+\ldots) \mid s_{t}=s\right]\\
&=\mathbb{E}\left[r_{t+1}+\gamma G_{t+1} \mid s_{t}=s\right]\\
&=\mathbb{E}\left[r_{t+1}|s_t=s\right] +\gamma \mathbb{E}\left[G_{t+1} \mid s_{t}=s\right]\\
&=R(s)+\gamma \mathbb{E}[G_{t+1}|s_t=s] \\
&=R(s)+\gamma \mathbb{E}[V(s_{t+1})|s_t=s]\\
&=R(s)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s\right) V\left(s^{\prime}\right)
\end{aligned}
V ( s ) = E [ G t ∣ s t = s ] = E [ r t + 1 + γ r t + 2 + γ 2 r t + 3 + … ∣ s t = s ] = E [ r t + 1 + γ ( r t + 2 + γ r t + 3 + … ) ∣ s t = s ] = E [ r t + 1 + γ G t + 1 ∣ s t = s ] = E [ r t + 1 ∣ s t = s ] + γ E [ G t + 1 ∣ s t = s ] = R ( s ) + γ E [ G t + 1 ∣ s t = s ] = R ( s ) + γ E [ V ( s t + 1 ) ∣ s t = s ] = R ( s ) + γ s ′ ∈ S ∑ P ( s ′ ∣ s ) V ( s ′ )
对 S S S { s 1 , s 2 , ⋯ , s n } \{s_1,s_2,\cdots,s_n\} { s 1 , s 2 , ⋯ , s n }
V ( s 1 ) = R ( s 1 ) + γ [ P s 1 s 1 V ( s 1 ) + P s 1 s 2 V ( s 2 ) + ⋯ + P s 1 s N V ( s N ) ] … … V ( s N ) = R ( s N ) + γ [ P s N s 1 V ( s 1 ) + P s N s 2 V ( s 2 ) + ⋯ + P s N s N V ( s N ) ] V(s_1)=R(s_1)+\gamma[P_{s_1s_1}V(s_1)+P_{s_1s_2}V(s_2)+\cdots+P_{s_1s_N}V(s_N)]\\
\ldots\\\ldots\\
V(s_N)=R(s_N)+\gamma[P_{s_Ns_1}V(s_1)+P_{s_Ns_2}V(s_2)+\cdots+P_{s_Ns_N}V(s_N)]
V ( s 1 ) = R ( s 1 ) + γ [ P s 1 s 1 V ( s 1 ) + P s 1 s 2 V ( s 2 ) + ⋯ + P s 1 s N V ( s N ) ] … … V ( s N ) = R ( s N ) + γ [ P s N s 1 V ( s 1 ) + P s N s 2 V ( s 2 ) + ⋯ + P s N s N V ( s N ) ]
可以把 Bellman Equation 写成一种矩阵的形式,如下式所示。
[ V ( s 1 ) V ( s 2 ) ⋮ V ( s N ) ] = [ R ( s 1 ) R ( s 2 ) ⋮ R ( s N ) ] + γ [ P ( s 1 ∣ s 1 ) P ( s 2 ∣ s 1 ) … P ( s N ∣ s 1 ) P ( s 1 ∣ s 2 ) P ( s 2 ∣ s 2 ) … P ( s N ∣ s 2 ) ⋮ ⋮ ⋱ ⋮ P ( s 1 ∣ s N ) P ( s 2 ∣ s N ) … P ( s N ∣ s N ) ] [ V ( s 1 ) V ( s 2 ) ⋮ V ( s N ) ] \left[\begin{array}{c}
V\left(s_{1}\right) \\
V\left(s_{2}\right) \\
\vdots \\
V\left(s_{N}\right)
\end{array}\right]=\left[\begin{array}{c}
R\left(s_{1}\right) \\
R\left(s_{2}\right) \\
\vdots \\
R\left(s_{N}\right)
\end{array}\right]+\gamma\left[\begin{array}{cccc}
P\left(s_{1} \mid s_{1}\right) & P\left(s_{2} \mid s_{1}\right) & \ldots & P\left(s_{N} \mid s_{1}\right) \\
P\left(s_{1} \mid s_{2}\right) & P\left(s_{2} \mid s_{2}\right) & \ldots & P\left(s_{N} \mid s_{2}\right) \\
\vdots & \vdots & \ddots & \vdots \\
P\left(s_{1} \mid s_{N}\right) & P\left(s_{2} \mid s_{N}\right) & \ldots & P\left(s_{N} \mid s_{N}\right)
\end{array}\right]\left[\begin{array}{c}
V\left(s_{1}\right) \\
V\left(s_{2}\right) \\
\vdots \\
V\left(s_{N}\right)
\end{array}\right]
⎣ ⎢ ⎢ ⎢ ⎢ ⎡ V ( s 1 ) V ( s 2 ) ⋮ V ( s N ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ R ( s 1 ) R ( s 2 ) ⋮ R ( s N ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ + γ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ P ( s 1 ∣ s 1 ) P ( s 1 ∣ s 2 ) ⋮ P ( s 1 ∣ s N ) P ( s 2 ∣ s 1 ) P ( s 2 ∣ s 2 ) ⋮ P ( s 2 ∣ s N ) … … ⋱ … P ( s N ∣ s 1 ) P ( s N ∣ s 2 ) ⋮ P ( s N ∣ s N ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ V ( s 1 ) V ( s 2 ) ⋮ V ( s N ) ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
由于 Bellman Equation 是线性方程,可以直接求解得解析解:
V = R + γ P V V = ( I − γ P ) − 1 R \begin{aligned}
V &= \mathcal{R}+ \gamma \mathcal{P}V \\
V&=(I-\gamma \mathcal{P})^{-1}\mathcal{R}
\end{aligned}
V V = R + γ P V = ( I − γ P ) − 1 R
但是 P \mathcal{P} P O ( n 3 ) O(n^3) O ( n 3 )
对于大规模 MRP 问题,可使用迭代和基于数据的方法,如动态规划、蒙特卡洛估计、时间差分等。
马尔可夫决策过程(Markov Decision Process, MDP)
相较于马尔科夫奖励过程,马尔科夫决策过程多了一个行为集合 A \mathcal{A} A
总体上 MDP 多了一个选则动作的过程,状态转移变成了 P s s ′ a = P ( s t + 1 = s ′ ∣ s t = s , a t = a ) \mathcal{P}_{ss^{\prime}}^a=\mathbb{P}\left(s_{t+1}=s^{\prime} \mid s_{t}=s, a_{t}=a\right) P s s ′ a = P ( s t + 1 = s ′ ∣ s t = s , a t = a ) R s a = R ( s t = s , a t = a ) = E [ r t + 1 ∣ s t = s , a t = a ] R_s^a=R\left(s_{t}=s, a_{t}=a\right)=\mathbb{E}\left[r_{t+1} \mid s_{t}=s, a_{t}=a\right] R s a = R ( s t = s , a t = a ) = E [ r t + 1 ∣ s t = s , a t = a ]
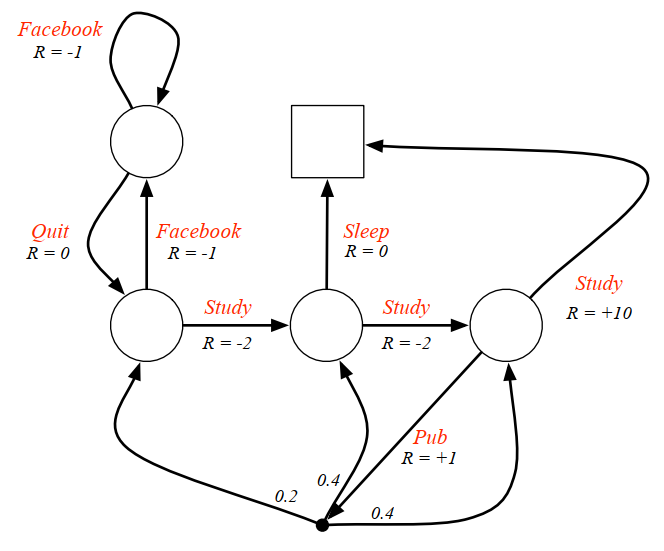
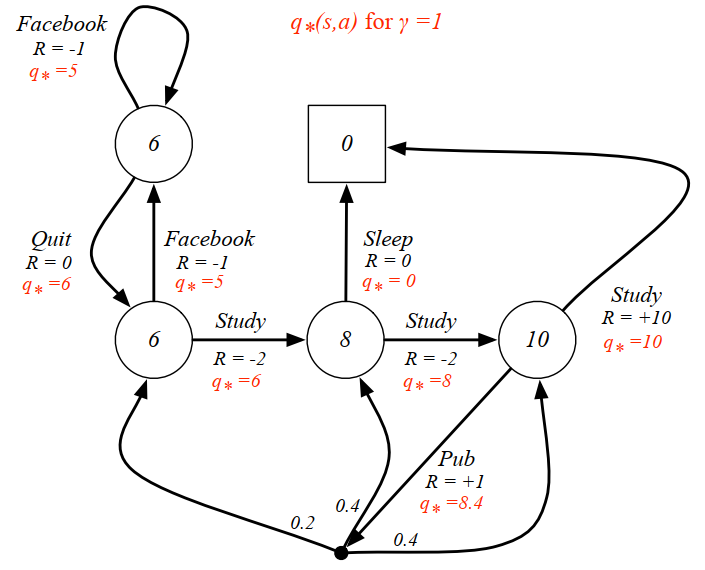
学生 MDP 例子:下图给出了一个可能的MDP的状态转化图。图中红色的文字表示的是采取的行为,而不是先前的状态名。对比之前的学生MRP示例可以发现,即时奖励与行为对应了,同一个状态下采取不同的行为得到的即时奖励是不一样的。由于引入了Action,容易与状态名混淆,此图没有给出各状态的名称;此图还把 Pass 和 Sleep 状态合并成一个终止状态;另外当选择”去查阅文献”这个动作时,主动进入了一个临时状态(图中用黑色小实点表示),随后被动的 被环境按照其动力学分配到另外三个状态,也就是说此时 Agent 没有选择权决定去哪一个状态。
策略(Policy): Policy 定义了在某一个状态应该采取什么样的动作。知道当前状态过后,把当前状态带入 policy function,然后就会得到一个概率,即
π ( a ∣ s ) = P ( a t = a ∣ s t = s ) \pi(a \mid s)=\mathbb{P}\left(a_{t}=a \mid s_{t}=s\right)
π ( a ∣ s ) = P ( a t = a ∣ s t = s )
一个策略完整定义了个体的行为方式,也就是说定义了个体在各个状态下的各种可能的行为方式以及其概率的大小。Policy 仅和当前的状态有关,与历史无关,满足马尔可夫性;同时某一给定的Policy是静态的,与时间无关,但是个体可以随着时间更新策略。而策略可能是确定性策略,即 π ( ⋅ ∣ s ) = 1 \pi(\cdot\mid s)=1 π ( ⋅ ∣ s ) = 1 π ( s ) \pi(s) π ( s ) s s s π ( s , a ) \pi(s,a) π ( s , a ) π ( a ∣ s ) \pi(a\mid s) π ( a ∣ s ) s s s a a a
已知一个 MDP 和一个 policy π \pi π
MDP 过程的价值函数
定义 V π ( s ) V_\pi(s) V π ( s ) π π π 状态价值函数 ,表示从状态 s s s π π π s s s
定义 Q π ( s , a ) Q_\pi(s,a) Q π ( s , a ) 动作价值函数 ,表示在当前状态 s s s a a a a a a π \pi π π \pi π π π π
贝尔曼期望方程(Bellman Expectation Eq)
MDP 下的状态价值函数和动作价值函数与 MRP 下的价值函数类似,可以用下一时刻状态价值函数或动作价值函数来表达。
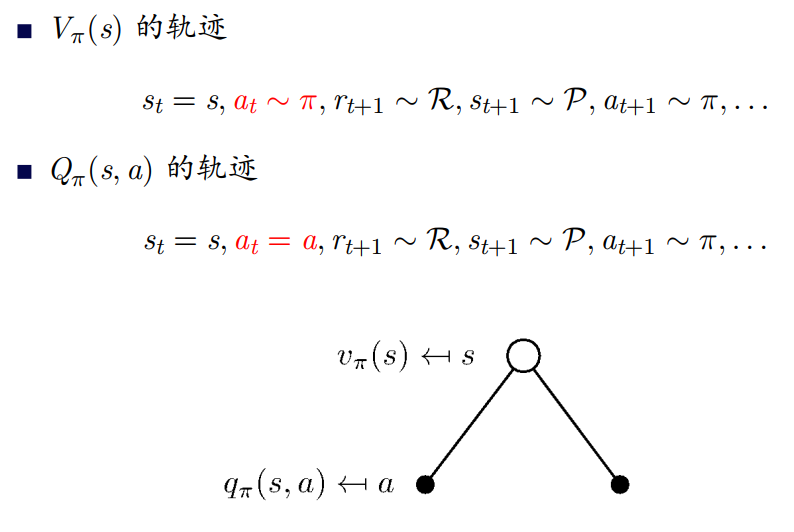
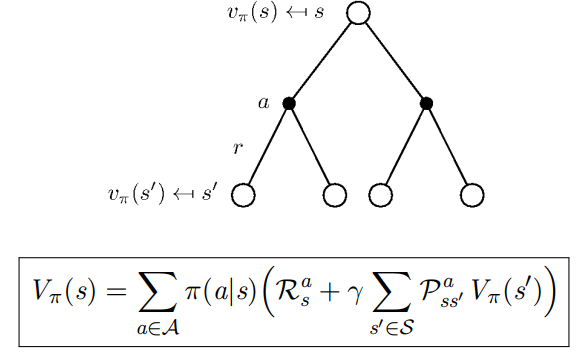
于是得到 V π ( s ) V_\pi(s) V π ( s ) Q π ( s , a ) Q_\pi(s,a) Q π ( s , a )
V π ( s ) = ∑ a ∈ A π ( a ∣ s ) Q π ( s , a ) V_{\pi}(s)=\sum_{a \in A} \pi(a \mid s) Q_{\pi}(s, a)
V π ( s ) = a ∈ A ∑ π ( a ∣ s ) Q π ( s , a )
上式表明,在遵循策略 π π π s s s
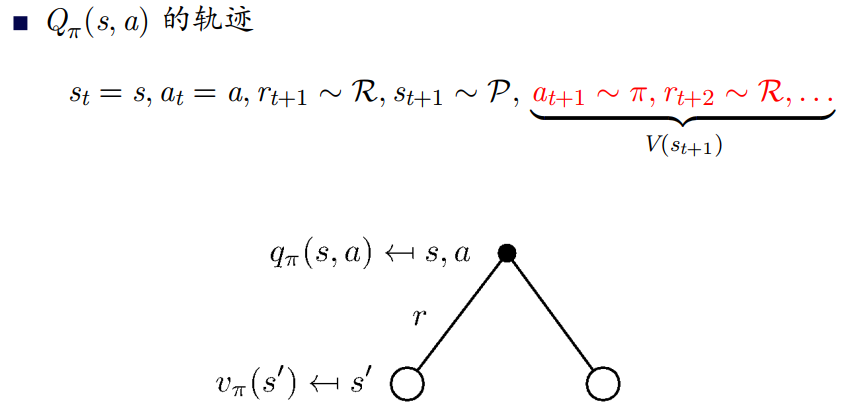
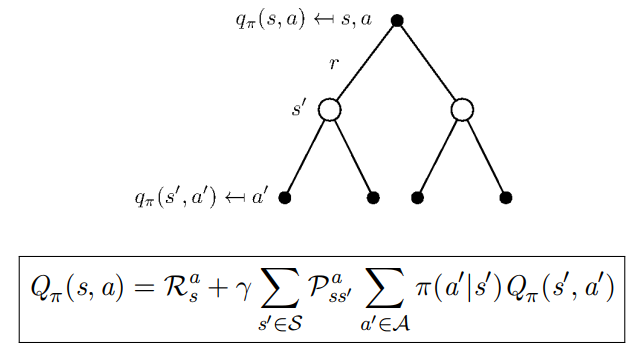
将 Q π ( s , a ) Q_{\pi}(s, a) Q π ( s , a ) V π ( s ) V_\pi(s) V π ( s )
Q π ( s , a ) = R s a + γ ∑ s ′ ∈ S P s s ′ a V π ( s ′ ) Q_{\pi}(s, a)=\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} V_{\pi}\left(s^{\prime}\right)
Q π ( s , a ) = R s a + γ s ′ ∈ S ∑ P s s ′ a V π ( s ′ )
上式表明某一个状态下的动作价值可以分为两部分:其一是离开这个状态的价值,其二是所有进入新的状态的价值于其转移概率乘积的和。更具体的:
Q π ( s , a ) = E [ G t ∣ s t = s , a t = a ] = E π [ r t + 1 + γ r t + 2 + γ 2 r t + 3 + … ∣ s t = s , a t = a ] = E π [ r t + 1 ∣ s t = s , a t = a ] + γ E π [ r t + 2 + γ r t + 3 + γ 2 r t + 4 + … ∣ s t = s , a t = a ] = R π ( s , a ) + γ E π [ G t + 1 ∣ s t = s , a t = a ] = R π ( s , a ) + γ E π [ V π ( s t + 1 ) ∣ s t = s , a t = a ] = R π ( s , a ) + γ ∑ s ′ ∈ S P ( s ′ ∣ s , a ) V π ( s ′ ) \begin{aligned}
Q_\pi(s,a)&=\mathbb{E}\left[G_{t} \mid s_{t}=s,a_{t}=a\right]\\
&=\mathbb{E}_\pi\left[r_{t+1}+\gamma r_{t+2}+\gamma^{2} r_{t+3}+\ldots \mid s_{t}=s,a_{t}=a\right] \\
&=\mathbb{E}_\pi\left[r_{t+1}|s_{t}=s,a_{t}=a\right] +\gamma \mathbb{E}_\pi\left[r_{t+2}+\gamma r_{t+3}+\gamma^{2} r_{t+4}+\ldots \mid s_{t}=s,a_{t}=a\right]\\
&=R_\pi(s,a)+\gamma \mathbb{E}_\pi[G_{t+1}|s_{t}=s,a_{t}=a] \\
&=R_\pi(s,a)+\gamma \mathbb{E}_\pi[V_\pi(s_{t+1})|s_{t}=s,a_{t}=a]\\
&=R_\pi(s,a)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s,a\right) V_\pi\left(s^{\prime}\right)
\end{aligned}
Q π ( s , a ) = E [ G t ∣ s t = s , a t = a ] = E π [ r t + 1 + γ r t + 2 + γ 2 r t + 3 + … ∣ s t = s , a t = a ] = E π [ r t + 1 ∣ s t = s , a t = a ] + γ E π [ r t + 2 + γ r t + 3 + γ 2 r t + 4 + … ∣ s t = s , a t = a ] = R π ( s , a ) + γ E π [ G t + 1 ∣ s t = s , a t = a ] = R π ( s , a ) + γ E π [ V π ( s t + 1 ) ∣ s t = s , a t = a ] = R π ( s , a ) + γ s ′ ∈ S ∑ P ( s ′ ∣ s , a ) V π ( s ′ )
回带,最终得到迭代形式的贝尔曼期望方程:
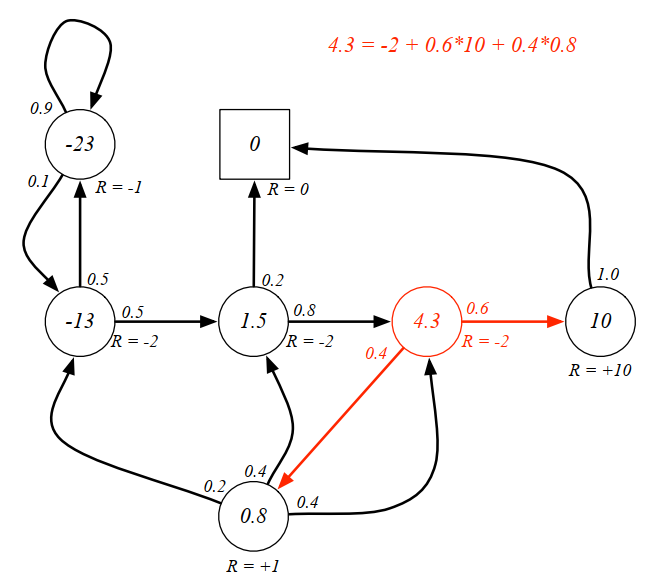
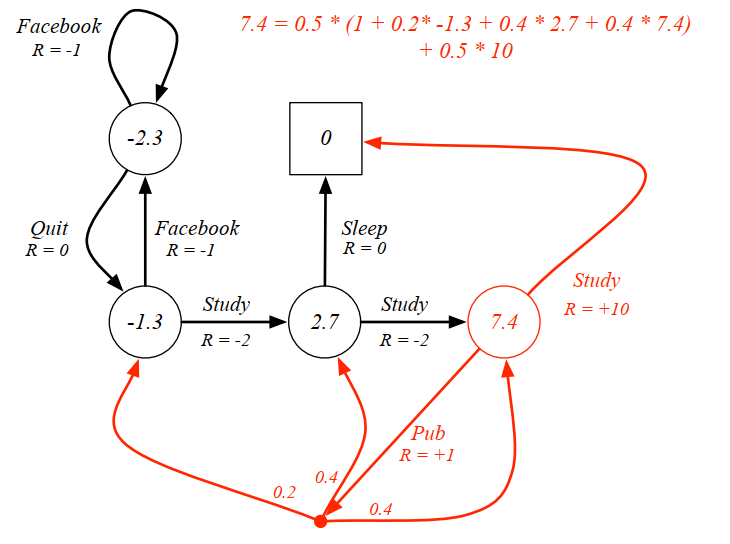
例子:下图是 γ = 1 \gamma=1 γ = 1 π ( a ∣ s ) = 0.5 \pi(a\mid s)=0.5 π ( a ∣ s ) = 0 . 5
贝尔曼期望方程同样可以写为矩阵形式:
V π = R π + γ P π V π V π = ( I − γ P π ) − 1 R π \begin{aligned}
V_\pi &= \mathcal{R}^\pi+ \gamma \mathcal{P}^\pi V_\pi \\
V_\pi&=(I-\gamma \mathcal{P}^\pi)^{-1}\mathcal{R}^\pi
\end{aligned}
V π V π = R π + γ P π V π = ( I − γ P π ) − 1 R π
贝尔曼最优方程(Bellman Optimal Equation)
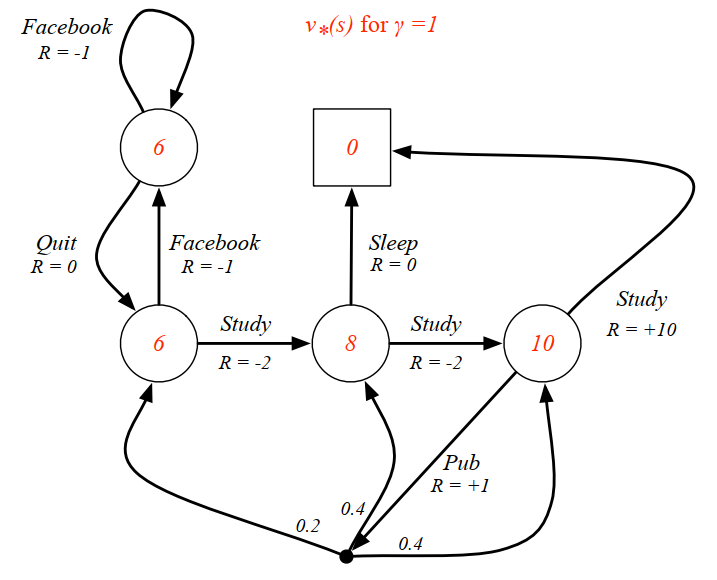
最优状态价值函数 V ∗ ( s ) V_*(s) V ∗ ( s ) s s s Q ∗ ( s , a ) Q_*(s,a) Q ∗ ( s , a ) s s s
如果我们知道最优的状态价值或最优策略,说明 MDP 问题被解决。
策略比较:π ≥ π ′ i f V π ( s ) ≥ V π ′ ( s ) , ∀ s π \geq π^{\prime} \quad if \quad V_π(s) \geq V_{\pi^{\prime}}(s),\quad \forall s π ≥ π ′ i f V π ( s ) ≥ V π ′ ( s ) , ∀ s
定理: 对任意 MDP 过程:(1) 存在一个最优策略 π ∗ \pi_* π ∗ π ∗ > π , ∀ π \pi_*>\pi,\forall \pi π ∗ > π , ∀ π V π ∗ ( s ) = V ∗ ( s ) V_{\pi_*}(s)=V_*(s) V π ∗ ( s ) = V ∗ ( s ) Q π ∗ ( s , a ) = Q ∗ ( s , a ) Q_{π_∗}(s, a) = Q_∗(s, a) Q π ∗ ( s , a ) = Q ∗ ( s , a )
对于 V ∗ V_* V ∗
$$
V_{*}(s)=\max _{a} Q_{*}(s, a)
$$
对于 $Q_*$ ,在某个状态 $s$ 下,采取某个动作的最优价值由 2 部分组成,一部分是离开状态 $s$ 的即时奖励,另一部分则是所有能到达的状态 $s’$ 的最优状态价值按出现概率求和:
Q ∗ ( s , a ) = R s a + γ ∑ s ′ ∈ S P s s ′ a V ∗ ( s ′ ) Q_{*}(s,a)=\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}}\mathcal{P}_{s s^{\prime}}^{a} V_*(s^{\prime})
Q ∗ ( s , a ) = R s a + γ s ′ ∈ S ∑ P s s ′ a V ∗ ( s ′ )
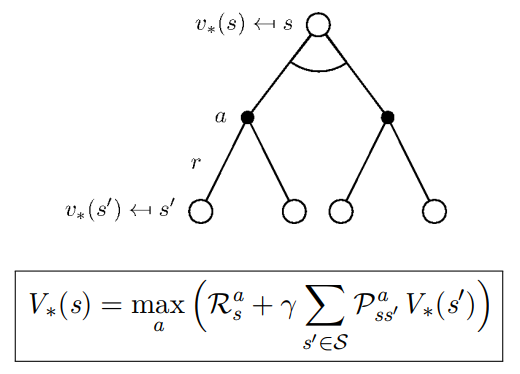
组合起来,对最优状态价值 V ∗ V_* V ∗
这可以看做使每一步达到最优的最终结果:
V ∗ ( s 0 ) = E [ max a 0 , a 1 , … ( r 1 + γ r 2 + γ 2 r 3 + … ) ] = E [ max a 0 ( r 1 + γ max a 1 , a 2 , … ( r 2 + γ r 3 + … ) ) ] = E [ max a 0 ( r 1 + γ ∑ s 1 P s 0 s 1 a 0 V ∗ ( s 1 ) ) ] = max a 0 ( R ( s 0 , a 0 ) + γ ∑ s 1 P s 0 s 1 a 0 V ∗ ( s 1 ) ) \begin{aligned}
V_{*}\left(s_{0}\right) &=\mathbb{E}\left[\max _{a_{0}, a_{1}, \ldots}\left(r_{1}+\gamma r_{2}+\gamma^{2} r_{3}+\ldots\right)\right] \\
&=\mathbb{E}\left[\max _{a_{0}}\left(r_{1}+\gamma \max _{a_{1}, a_{2}, \ldots}\left(r_{2}+\gamma r_{3}+\ldots\right)\right)\right] \\
&=\mathbb{E}\left[\max _{a_{0}}\left(r_{1}+\gamma \sum_{s_{1}} \mathcal{P}_{s_{0} s_{1}}^{a_{0}} V_{*}\left(s_{1}\right)\right)\right] \\
&=\max _{a_{0}}\left(\mathcal{R}\left(s_{0}, a_{0}\right)+\gamma \sum_{s_{1}} \mathcal{P}_{s_{0} s_{1}}^{a_{0}} V_{*}\left(s_{1}\right)\right)
\end{aligned}
V ∗ ( s 0 ) = E [ a 0 , a 1 , … max ( r 1 + γ r 2 + γ 2 r 3 + … ) ] = E [ a 0 max ( r 1 + γ a 1 , a 2 , … max ( r 2 + γ r 3 + … ) ) ] = E [ a 0 max ( r 1 + γ s 1 ∑ P s 0 s 1 a 0 V ∗ ( s 1 ) ) ] = a 0 max ( R ( s 0 , a 0 ) + γ s 1 ∑ P s 0 s 1 a 0 V ∗ ( s 1 ) )
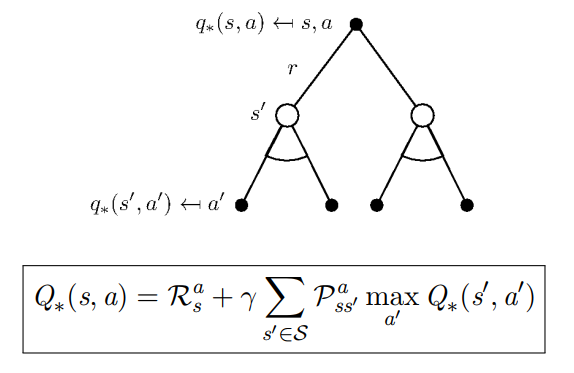
对最优动作价值 Q ∗ Q_* Q ∗
直觉上讲,贝尔曼最优方程表达了这样一个事实:最佳策略下的一个状态的价值必须等于在这个状态下采取最好动作得到的回报的期望。
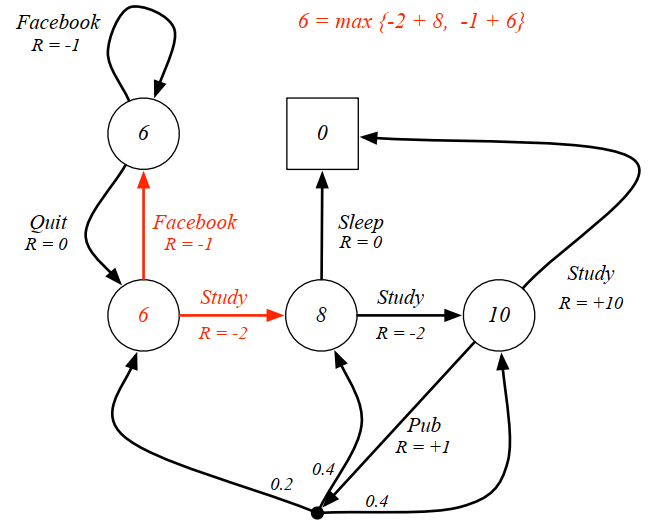
最优策略可以基于 V ∗ V_* V ∗
π ∗ ( s ) = arg max a ( R s a + γ ∑ s ′ ∈ S P s s ′ a V ∗ ( s ′ ) ) \pi_{*}(s)=\arg \max _{a}\left(\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} V_{*}\left(s^{\prime}\right)\right)
π ∗ ( s ) = arg a max ( R s a + γ s ′ ∈ S ∑ P s s ′ a V ∗ ( s ′ ) )
为了方便,也可以直接最大化 Q ∗ ( s , a ) Q_*(s,a) Q ∗ ( s , a )
π ∗ ( s ) = arg max a Q ∗ ( s , a ) \pi_{*}(s)=\arg \max _{a} Q_{*}(s, a)
π ∗ ( s ) = arg a max Q ∗ ( s , a )
这是一个确定型最优策略:
π ∗ ( a ∣ s ) = { 1 , i f a = a r g m a x a ∈ A Q ∗ ( s , a ) 0 , o t h e r w i s e \pi_{*}(a\mid s)=\begin{cases}
1,\quad if\ a=\mathop{argmax}_{a\in \mathcal{A}} Q_{*}(s, a)\\
0,\quad otherwise
\end{cases}
π ∗ ( a ∣ s ) = { 1 , i f a = a r g ma x a ∈ A Q ∗ ( s , a ) 0 , o t h e r w i s e
对于任何MDP问题,总存在一个确定性的最优策略。
求解贝尔曼最优方程:Bellman最优方程是非线性的,没有固定的解决方案,通过一些迭代方法来解决:价值迭代、策略迭代、Q学习、Sarsa等。
Q.E.D.


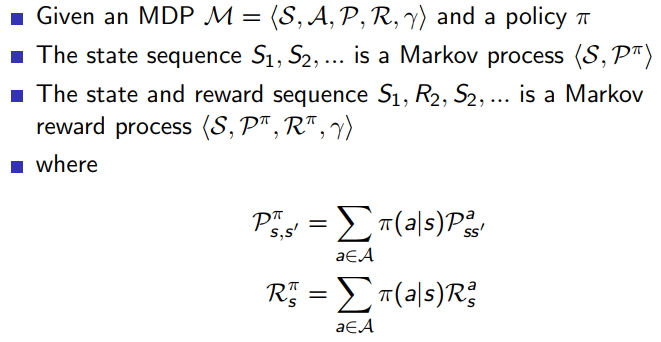


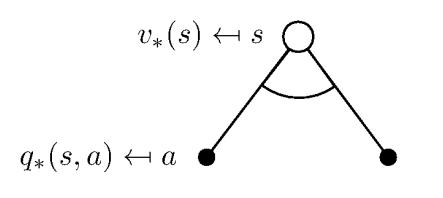 $$
V_{*}(s)=\max _{a} Q_{*}(s, a)
$$
对于 $Q_*$ ,在某个状态 $s$ 下,采取某个动作的最优价值由 2 部分组成,一部分是离开状态 $s$ 的即时奖励,另一部分则是所有能到达的状态 $s’$ 的最优状态价值按出现概率求和:
$$
V_{*}(s)=\max _{a} Q_{*}(s, a)
$$
对于 $Q_*$ ,在某个状态 $s$ 下,采取某个动作的最优价值由 2 部分组成,一部分是离开状态 $s$ 的即时奖励,另一部分则是所有能到达的状态 $s’$ 的最优状态价值按出现概率求和: