计数 DP

count(n, x) 表示 1~n 中 x 出现的次数。则 a~b 中 x 出现的次数即 count(b, x) - count(a - 1, x) 。

求 1~n 中，x 出现的次数：
例如：n=abcdefg ， 求x在第4位出现的次数(低到高)
分类讨论：
①前三位：000_{abc-1,x,后三位000}999. 方案数:abc*1000
②前三位：abc,x
…2.1 d < x , 后三位：无解. 方案数：0
…2.2 d = x , 后三位：000~dfg. 方案数:dfg+1
…2.3 d > x , 后三位：000~999. 方案数:1000

注意：

1. 当判断 x 在第 1 位出现的次数时，不存在情况 ①

2. 当 x=0 且在情况 ① 时，因为不能前导全 0，因此得从 001 开始，(这一步特判即可)

#include <iostream>
#include <vector>
using namespace std;
int get(vector<int>num, int l, int r){
    int res = 0;
    for(int i = l; i >= r; i --)
        res = res * 10 + num[i];
    return res;
}
int power10(int x){
    int res = 1;
    while(x --) res *= 10;
    return res;
}
int count(int n, int x){
    if(n == 0) return 0;
    vector<int>num;
    while(n){// n 的每一位存入 vector, 低位在前，高位在后
        num.push_back(n % 10);
        n /= 10;
    }
    n = num.size();
    int res = 0;
    for(int i = n - 1 - !x; i >= 0; i --){ // x == 0, i == n-1 的无需计算，所在位不能为最高位的 0
        if(i < n - 1){ // i == n - 1 时情况 1 不存在,无需计算,i<n-1 才计算情况1
            res += get(num, n - 1, i + 1) * power10(i);
            if(x == 0) res -= power10(i);// x==0 时从001开始，因此减去多加的 10^i
        }
        if(num[i] > x) res += power10(i);
        else if(num[i] == x) res += get(num, i - 1, 0) + 1;
    }
    return res;
}
int main(){
    int a, b; 
    while(cin >> a >> b, a || b){
        if(a > b) swap(a, b);
        for(int i = 0; i < 10; i ++)
            cout << count(b, i) - count(a - 1, i) << " ";
        cout << endl;
    }
}

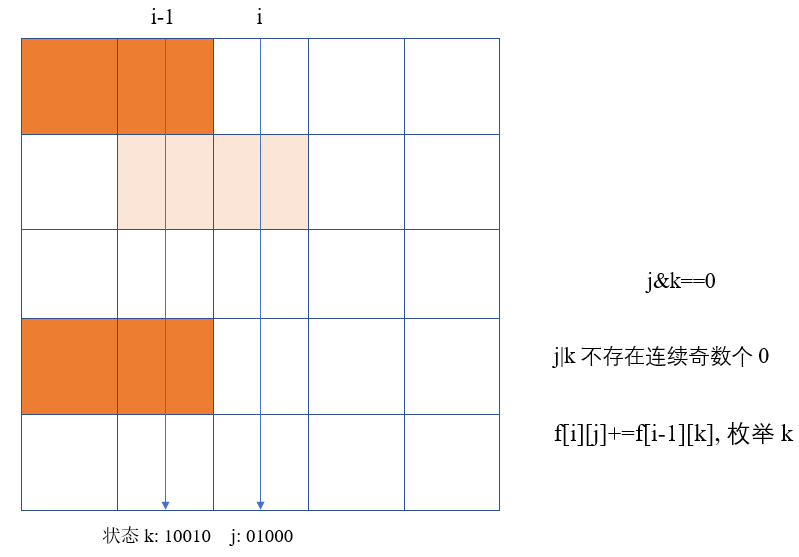
状态压缩 DP

$f[i][j]$ 表示第 $i$ 列状态为 $j$ 时前 $i$ 列分割方案的总数，状态 $j$ 是上一列的填充延伸到当前列的二进制表示。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 12, M = 1 << N;
int n, m;
long long f[N][M];
int st[M];
int main(){
    while(cin >> n >> m, n || m){
        memset(f, 0, sizeof f); // 因为多次计算，清空上次结果
        for(int i = 0; i < 1 << n; i ++){ // 预处理 st, 每个二进制状态是否可用
            // 如 10001, 11000 这样的不可用
            st[i] = 1;
            int cnt = 0; // 连续 0 的个数
            for(int j = 0; j < n; j ++)
                if(i >> j & 1){
                    if(cnt & 1) st[i] = 0; // 连续奇数个 0 状态不可用
                    cnt = 0;
                } else cnt ++;
            if(cnt & 1) st[i] = 0;
		}
        f[0][0] = 1;// f[0][k] = 0; 注意 f[i][j] 的定义, f[0][0] 这种情况存在; f[0][k], k!=0, 这种情况不存在，-1 列不可能有方格延伸到 0。
        for(int i = 1; i <= m; i ++) // 枚举列 i
            for(int j = 0; j < 1 << n; j ++) // 枚举列的每个状态
                for(int k = 0; k < 1 << n; k ++) // 枚举上一列的状态
                    if((j & k) == 0 && st[j | k])
                        f[i][j] += f[i-1][k];
        cout << f[m][0];// m列不放小方格，前m-1列已经完全摆放好并且不伸出来的状态
    }
}

最短哈密顿路径：

$f[i][j]$ 表示从 0 走到 j ，经过的点的状态是 i 的所有路径最小值。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20, M = 1 << N;
int n;
int w[N][N]; // w 是邻接矩阵
int f[M][N];
int main(){
	cin >> n;
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < n; j ++)
            cin >> w[i][j];
    memset(f, 0x3f, sizeof f);
    f[1][0] = 0; // 初始访问状态为0号顶点被访问,路径长度为0
    for(int i = 0; i < 1 << n; i ++)
        for(int j = 0; j < n; j ++) // 走到点 j
            if(i >> j & 1) // 
                for(int k = 0; k < n; k ++) // k表示走到j的前一个点,以k为终点的最短距离
                    if((i - (1 << j)) >> k & 1) // 等价 if(k !=j && (i >> k) & 1)
                        f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
    cout << f[(1 << n) - 1][n - 1]; // 所有点都走过
}

树形 DP

树形 DP 的关键是要求解时，一次可求得两个状态。

$f[i][j],j=0,1$ 表示以 $i$ 为根的树中邀请人参加舞会幸福指数的最大值，$j=1$ 表示根节点参加，$j=0$ 表示根节点不参加。

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 6010;
int n;
int happy[N];
int h[N], e[N], ne[N], idx;
int f[N][2];
int has_father[N];
void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u){
    f[u][1] = happy[u];
    for(int i = h[u]; i != -1; i = ne[i]){
        int j = e[i];
        dfs(j);
        f[u][0] += max(f[j][0], f[j][1]);
        f[u][1] += f[j][0];
    }
}
int main(){
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> happy[i];
    memset(h, -1, sizeof h);
    for(int i = 0; i < n - 1; i ++){
        int a, b;
        cin >> a >> b;
        has_father[a] = 1;
        add(b, a);
    }
    int root = 1;
    while(has_father[root]) root ++;
    dfs(root);
    cout << max(f[root][0], f[root][1]) << endl; 
}

记忆化搜索

动态规划的递归求解法。记忆化搜索的关键是：

如果已求解过则直接返回 $f[i][j]$；

否则 dfs 继续下去，最后返回 $f[i][j]$;

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 310;
int n, m;
int h[N][N], f[N][N];
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};

int dfs(int x, int y){
    int &v = f[x][y];
    if(v != -1) return v;
    v = 1; // 至少可以滑动 1 格，即 1
    for(int i = 0; i < 4; i ++){
        int a = x + dx[i], b = y + dy[i];
        if(a >= 1 && a <= n && b >= 1 && b <= m && h[a][b] < h[x][y])
            v = max(v, dfs(a, b) + 1);
    }
    return v;
}
int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            cin >> h[i][j];
    memset(f, -1, sizeof f); 
    int res = 0;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            res = max(res, dfs(i, j));
    cout << res;
}

Q.E.D.