算法基础课（十三）——线性DP与区间DP

2020-06-17   

线性 DP 与区间 DP

// 数字三角形, 自顶向下
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, INF = 1e9;
int a[N][N], f[N][N];
int main(){
    int n; cin >> n;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= i; j ++)
            cin >> a[i][j];
    for(int i = 1; i <= n; i ++)
        for(int j = 0; j <= i + 1; j ++) // 注意初始化陷阱
            f[i][j] = -INF;
        
    f[1][1] = a[1][1];
    for(int i = 2; i <= n; i ++)
        for(int j = 1; j <= i; j ++)
            f[i][j] = max(f[i-1][j-1], f[i-1][j]) + a[i][j];
    int res = - INF;
    for(int i = 1; i <= n; i ++) res = max(res, f[n][i]);
    cout << res;
}

// 数字三角形, 自底向上
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, INF = 1e9;
int f[N][N];
int main(){
    int n; cin >> n;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= i; j ++)
            cin >> f[i][j];
    
    for(int i = n - 1; i >= 1; i --)
        for(int j = 1; j <= i; j ++){
            f[i][j] = max(f[i+1][j], f[i+1][j+1]) + f[i][j];
        }
            
    cout << f[1][1];
}

LIS 问题：

// O(n^2)
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, a[N], f[N];
int main(){
	cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1; i <= n; i ++){
        f[i] = 1;
        for(int j = 1; j < i; j ++)
            if(a[j] < a[i])
                f[i] = max(f[i], f[j] + 1);
    }
    int res = 0;
    for(int i = 1; i <= n; i ++) res = max(res, f[i]);
    cout << res;
}

// 长度为 k 的上升子序列只需要存储结尾值最小的那个。
// O(n log n) 二分
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, a[N];
int q[N]; // 不同长度上升子序列结尾最小值, 存的最终不一定是 LIS
int main(){
    cin >> n;
    for(int i = 0; i < n; i ++) cin >> a[i];
    int len = 0;
    q[0] = -2e9;
    for(int i = 0; i < n; i ++){
        int l = 0, r = len;
        while(l < r){
            int mid = l + r + 1 >> 1;
            if(q[mid] < a[i]) l = mid;
            else r = mid - 1;
        } // 求 < a[i] 的最大值
        len = max(len, r + 1);
        q[r + 1] = a[i];
    }
    cout << len;
}

// 单调栈, O(n log n)
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int stk[N], cnt = -1; // 注意最终 stk 存的不一定是 LIS
int a[N], n;
int main(){
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    stk[++ cnt] = a[1];
    for(int i = 2; i <= n; i ++){
        if(a[i] > stk[cnt]) stk[++ cnt] = a[i];//如果该元素大于栈顶元素,将该元素入栈
        else{ //替换掉第一个大于或者等于这个数字的那个数
            int t = lower_bound(stk, stk + cnt + 1, a[i]) - stk;
            stk[t] = a[i];
        } // *lower_bound(stk, stk + cnt + 1, a[i]) = a[i];
    }
    cout << cnt + 1;
}

// LIS 方案
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N], g[N];
int main(){
	cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1; i <= n; i ++){
        f[i] = 1;
        for(int j = 1; j < i; j ++)
            if(a[j] < a[i]){
                if(f[j] + 1 > f[i]){
                    f[i] = f[j] + 1;
                    g[i] = j;
                }
            }
    }
    int k = 1;
    for(int i = 1; i <= n; i ++) 
        if(f[k] < f[i]) k = i;
    cout << f[k] << endl;
    for(int i = 0, len = f[k]; i < len; i ++){
        cout << k << " " << a[k] << " " << endl; // 注意输出是逆序的，实际可能要 reverse 一下
        k = g[k];
    }
}

实际上 f[]f[] 的求解结果也隐含了路径信息。

// 单调栈, O(n log n)
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int stk[N], cnt = -1; // 注意最终 stk 存的不一定是 LIS
int a[N], n, f[N];
int main(){
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    stk[++ cnt] = a[1];
    f[1] = 1;
    for(int i = 2; i <= n; i ++){
        if(a[i] > stk[cnt]) {
        	stk[++ cnt] = a[i];//如果该元素大于栈顶元素,将该元素入栈
            f[i] = cnt + 1;
        }
        else{ //替换掉第一个大于或者等于这个数字的那个数
            int t = lower_bound(stk, stk + cnt + 1, a[i]) - stk;
            stk[t] = a[i];
            f[i] = t + 1;
        } // *lower_bound(stk, stk + cnt + 1, a[i]) = a[i];
    }
    cout << cnt + 1 << endl;
    for(int i = n, len = cnt + 1; len >= 1; i --){
        if(f[i] == len){
            cout << a[i];
            len --;
        }
    }
}

LCS 问题：

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main(){
    cin >> n >> m;
    cin >> a +1 >> b + 1;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++){
            f[i][j] = max(f[i-1][j], f[i][j-1]);
            if(a[i] == b[j]) f[i][j] = max(f[i][j], f[i-1][j-1] + 1);
        }
    cout << f[n][m];
}

img

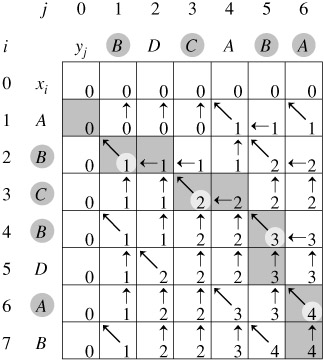
// LCS 方案
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int g[N][N]; // 记录当前状态由哪一种状态转移而来
int f[N][N];
string ans_str;

void get_string(int n, int m){
    if(!n || !m) return;
    if(g[n][m] == 0){
        // cout << a[n]; 
        ans_str += a[n];
        get_string(n - 1, m - 1);
    }else if(g[n][m] == 1) get_string(n, m - 1);
    else get_string(n - 1, m);
}
int main(){
    cin >> n >> m;
    cin >> a +1 >> b + 1;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++){
            if(f[i-1][j] > f[i][j]) f[i][j] = f[i-1][j], g[i][j] = -1;
            if(f[i][j-1] > f[i][j]) f[i][j] = f[i][j-1], g[i][j] = 1;
            if(a[i] == b[j]) {
                if(f[i-1][j-1] + 1 > f[i][j]) f[i][j] = f[i-1][j-1] + 1, g[i][j] = 0;
            }
        }
    cout << f[n][m] << endl;
    get_string(n, m);
    cout << ans_str; // 注意这里回溯得到的是逆序
}

LCIS 问题：

// 暴力
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3030;
int a[N], b[N];
int f[N][N];
int n, m;
void df(){
    for (int i = 1; i <= n; i ++ ){
    	for (int j = 1; j <= n; j ++ ){
        	f[i][j] = f[i - 1][j];
        	if (a[i] == b[j]){
            	int maxv = 1;
            	for (int k = 1; k < j; k ++ ){
                	if (a[i] > b[k])
                    	maxv = max(maxv, f[i - 1][k] + 1);
                }
            	f[i][j] = max(f[i][j], maxv);
        	}
    	}
	}
}

}
int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1; i <= m; i ++) cin >> b[i];
    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= m; j ++){
            f[i][j] = f[i-1][j];
            if(a[i] == b[j]){
                for(int k = 0; k < j; k ++){
                    if(b[k] < a[i]){
                        f[i][j] = max(f[i][j], f[i-1][k] + 1);
                    }
                }
            }
        }
    }
    int maxv = 0;
    for(int i = 1; i <= m; i ++) maxv = max(maxv, f[n][i]);
    cout << maxv;
}

void df(){
	for(int i = 1; i <= n; i ++){
        int maxv = 1;
        for(int j = 1; j <= m; j ++){
            f[i][j] = f[i-1][j];
            if(a[i] > b[j]) maxv = max(maxv, f[i][j]);
            if(a[i] == b[j]) f[i][j] = max(maxv, f[i-1][j] + 1);
        }
    }
}

编辑距离：

f[i][j]f[i][j] 把 a 的前 ii 个字符变成 b 的前 jj 个字符需要的最少操作。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
char a[N], b[N];
int f[N][N];
int n, m;
int main(){
    cin >> n; cin >> a + 1;
    cin >> m; cin >> b + 1;
    for(int i = 0; i <= n; i ++) f[i][0] = i;
    for(int i = 0; i <= m; i ++) f[0][i] = i;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++){
            f[i][j] = min(f[i-1][j], f[i][j-1]) + 1;
            if(a[i] == b[j]) f[i][j] = min(f[i][j], f[i-1][j-1]);
            else f[i][j] = min(f[i][j], f[i-1][j-1] + 1);
        }
    cout << f[n][m];
}


#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010, M = 15;
char str[N][M];
int n, m;
int f[M][M];
int edit_distance(char a[], char b[]){
    int la = strlen(a + 1), lb = strlen(b + 1);
    for(int i = 0; i <= la; i ++) f[i][0] = i;
    for(int i = 0; i <= lb; i ++) f[0][i] = i;
    for(int i = 1; i <= la; i ++)
        for(int j = 1; j <= lb; j ++){
            f[i][j] = min(f[i-1][j], f[i][j-1]) + 1;
            f[i][j] = min(f[i][j], f[i-1][j-1] + (a[i] != b[j]));
        }
    return f[la][lb];
}

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> str[i] + 1;
    while(m --){
        char s[M]; 
        int t;
        cin >> s + 1 >> t;
        int res = 0;
        for(int i = 1; i <= n; i ++)
            if(edit_distance(str[i], s) <= t) res ++;
        cout << res << endl;
    }
}

区间 DP：

#include <iostream>
#include <algorithm>
using namespace std;
const int N =307;
int n, s[N], f[N][N];
int main(){
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> s[i];
    for(int i = 1; i <= n; i ++) s[i] += s[i-1];
    for(int len = 2; len <= n; len ++) // 枚举长度
        for(int i = 1; i + len - 1 <= n; i ++){ // 枚举起点
            int l = i, r = i + len - 1;
            f[l][r] = 1e8;
            for(int k = l; k < r; k ++){ // 枚举分界点
                f[l][r] = min(f[l][r], f[l][k] + f[k+1][r] + s[r] - s[l-1]);
            }
        }
    cout << f[1][n];        
}

整数拆分：

和完全背包问题类似，f[i][j]f[i][j] 表示 1,2,...,i1,2,...,i 恰好拼成 jj 的方案数。于是，可以选 0 个 ii，1个 ii ，2 个 ii ……，把这些加起来即可。即：

f[i][j] = f[i-1][j] + f[i-1][j-i] + f[i-1][j-2i]+...+f[i-1][j-k*i]
f[i][j-i] =           f[i-1][j-i] + f[i-1][j-2i]+...+f[i-1][j-k*i]
于是有： f[i][j] = f[i-1][j] + f[i][j-i] 

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int f[N][N], n;
int main(){
    cin >> n;
    for(int i = 0; i <= n; i ++) f[i][0] = 1; // 拼成数 0, 只有不选一种方案
    for(int i = 1; i <= n; i ++)
        for(int j = 0; j <= n; j ++){
            f[i][j] = f[i-1][j];
            if(j >= i)
                f[i][j] = (f[i-1][j] + f[i][j-i]) % mod;
        }
    cout << f[n][n];
}

同样可以优化为 1 维：

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int f[N], n;
int main(){
    cin >> n;
    f[0] = 1; // 拼成数 0, 只有不选一种方案
    for(int i = 1; i <= n; i ++)
        for(int j = i; j <= n; j ++)
                f[j] = (f[j] + f[j-i]) % mod;
    cout << f[n];
}

另一种划分方式：所有总和是 ii 且恰好表示成 jj 个数的和的方案，f[i][j]f[i][j]。可分为两大类，方案中最小值是 1 和最小值大于 1 的。

最小值是 1 的，拿掉一个 1，可以一一对应到 f[i−1][j−1]f[i-1][j-1]；而最小值大于 1 的，每个数减去 1，可以一一对应到 f[i−j][j]f[i-j][j] 。于是 f[i][j]=f[i−1][j−1]+f[i−j][j]f[i][j]=f[i-1][j-1]+f[i-j][j] 。

最终 ans=f[n][1]+...+f[n][n]ans=f[n][1]+...+f[n][n] 。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int f[N][N], n;
int main(){
    cin >> n;
    f[0][0] = 1;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= i; j ++)
            f[i][j] = (f[i-1][j-1] +f[i-j][j]) % mod;
    int res = 0;
    for(int i = 1; i <= n; i ++) res = (res + f[n][i]) % mod;
    cout << res;
}

压位高精度

加法一般压 9 位，乘法压 4 位，乘法压 5 位相乘会爆 int 。

加法：

#include <iostream>
#include <vector>
using namespace std;
const int base = 1e9;
vector<int>add(vector<int>&A, vector<int>&B){
    vector<int>C;
    int t = 0;
    for(int i = 0; i < A.size() || t; i ++){
        if(i < A.size()) t += A[i];
        if(i < B.size()) t += B[i];
        C.push_back(t % base);
        t /= base;
    }
    return C;
}
int main(){
    string a, b; cin >> a >> b;
    vector<int>A, B;
    for(int i = a.size() - 1, s = 0, k = 0, t = 1; i >= 0; i --) {
        s += (a[i] - '0') * t; 
        k ++, t *= 10;
        if(k == 9 || i == 0){ // 共压 k = 9 位
            A.push_back(s);
            s = k = 0;
            t = 1;
        }
    }
    for(int i = b.size() - 1, s = 0, k = 0, t = 1; i >= 0; i --) {
        s += (b[i] - '0') * t;
        k ++, t *= 10;
        if(k == 9 || i == 0){
            B.push_back(s);
            s = k = 0;
            t = 1;
        }
    }
    auto C = add(A, B);
    cout << C.back(); // 避免了可能加入的前导 0
    for(int i = C.size() - 2; i >= 0; i --) printf("%09d", C[i]);
}

Q.E.D.

我是星，利剑开刃寒光锋芒的银星，绝不消隐