扩散模型笔记

2023-02-14   

扩散模型笔记

扩散模型的灵感来自于非平衡热力学。他们定义了一个扩散步骤的马尔可夫链，慢慢地向数据添加随机噪声，然后学习反向扩散过程，从噪声中构建所需的数据样本。与VAE或flow模型不同，扩散模型的学习过程是固定的，潜变量具有高维数(与原始数据相同)。通俗一点来说就是，现在我们的目标是用随机噪声生成原始数据，然而一步到位不太可能，于是我们将过程拆解，先分析原始数据是怎么一步步变为随机噪声的，再研究如何从噪声一步步恢复原样本。(拆楼与建楼)

img

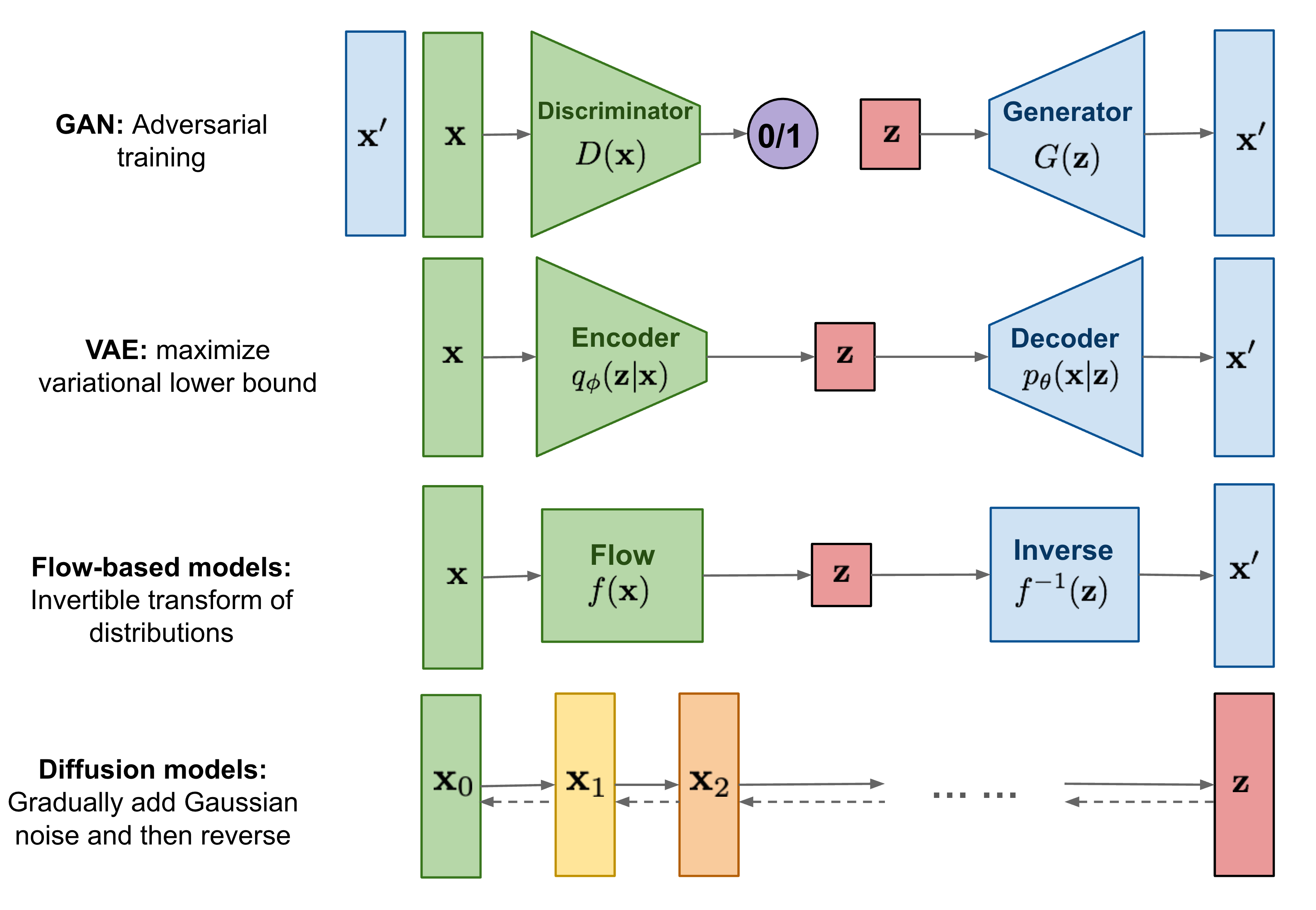
前向扩散过程

给定一个从真实数据分布中采样的数据点 x0∼q(x)\mathbf{x}_0 \sim q(\mathbf{x}) ，定义一个前向扩散过程，在这个过程中我们逐步向样本中分 TT 步添加少量的高斯噪声，产生一系列噪声样本 x1,…,xT\mathbf{x}_1, \dots, \mathbf{x}_T ，步长由一系列超参数 βt\beta_t 控制 {βt∈(0,1)}t=1T\{\beta_t \in (0, 1)\}_{t=1}^T ，通常我们会慢慢地增加 βt\beta_t ，也就是开始加入很小的噪声，随着时间步增加，加入的噪声慢慢变大：

q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)q(x1:T∣x0)=∏t=1Tq(xt∣xt−1)q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) \quad q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1})

数据点 x0\mathbf{x}_0 随着时间步 tt 的增加逐渐变的模糊不可分辨。最终当 T→∞T\rightarrow \infty ，xT\mathbf{x}_T 等价于各向同性高斯分布

img

下面我们就来具体看一下前向过程，前向过程一个非常不错的性质是我们可以取样在任意时间步 tt 对应的 xt\mathbf{x}_t (通过重参数化技巧)，定义 αt=1−βt\alpha_t = 1 - \beta_t 和 αˉt=∏i=1tαi\bar{\alpha}_t = \prod_{i=1}^t \alpha_i ：

xt=αtxt−1+1−αtϵt−1 ;其中 ϵt−1,ϵt−2,⋯∼N(0,I)=αtαt−1xt−2+1−αtαt−1ϵˉt−2=…=αˉtx0+1−αˉtϵq(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)\begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1} & \text{ ;其中 } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\boldsymbol{\epsilon}}_{t-2} & \\ &= \dots \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon} \\ q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) \end{aligned}

正态分布 N(0,σ12I)\mathcal{N}(\mathbf{0}, \sigma_1^2\mathbf{I}) 和 N(0,σ22I)\mathcal{N}(\mathbf{0}, \sigma_2^2\mathbf{I}) 的叠加分布为 N(0,(σ12+σ22)I)\mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2)\mathbf{I}) 。

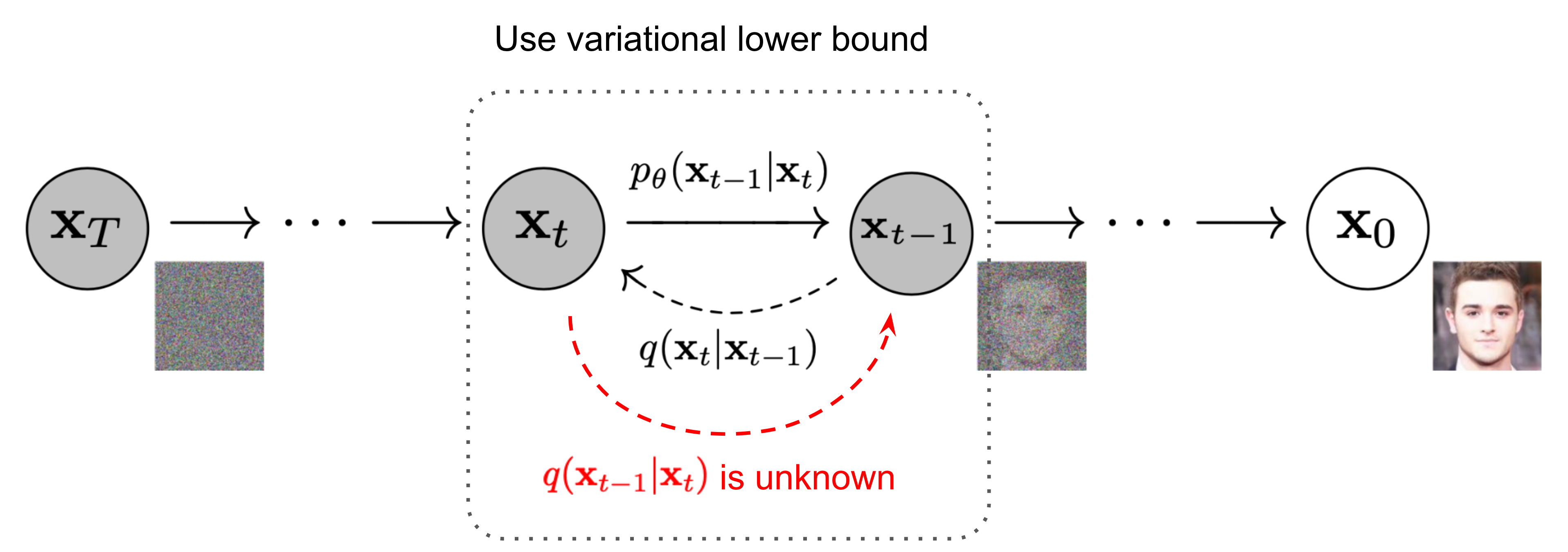
逆扩散过程

有了前向扩散过程，即加噪声破坏原始数据，现在我们考虑如何学习从噪声 xT∼N(0,I)\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) 开始一步步恢复数据，即学习 q(xt−1∣xt)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) ，那么最终我们就可以重建原数据。可以把逆扩散过程也建模为高斯，实际上如果 βt\beta_t 足够小，q(xt−1∣xt)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 也将是一个高斯分布。不过，估计 q(xt−1∣xt)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 并是一件容易的事情，因为它需要使用整个数据集，需要学习一个模型来近似这些条件概率以便进行逆扩散过程：

pθ(x0:T)=p(xT)∏t=1Tpθ(xt−1∣xt)pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T) \prod^T_{t=1} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \quad p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))

img

我们首先尝试计算逆扩散过程条件概率，逆扩散条件概率在已知 x0\mathbf{x}_0 的条件下是可以计算的：

q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \color{blue}{\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0), \color{red}{\tilde{\beta}_t} \mathbf{I})

使用贝叶斯公式以及马尔可夫性：

q(xt−1∣xt,x0)=exp⁡(−12((αtβt+11−αˉt−1)xt−12−(2αtβtxt+2αˉt−11−αˉt−1x0)xt−1+C(xt,x0)))\begin{aligned} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= \exp\Big( -\frac{1}{2} \big( \color{red}{(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2 - \color{blue}{(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1} \color{black}{ + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)} \end{aligned}

q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt−1∣x0)q(xt∣x0)∝exp⁡(−12((xt−αtxt−1)2βt+(xt−1−αˉt−1x0)21−αˉt−1−(xt−αˉtx0)21−αˉt))=exp⁡(−12(xt2−2αtxtxt−1+αtxt−12βt+xt−12−2αˉt−1x0xt−1+αˉt−1x021−αˉt−1−(xt−αˉtx0)21−αˉt))=exp⁡(−12((αtβt+11−αˉt−1)xt−12−(2αtβtxt+2αˉt−11−αˉt−1x0)xt−1+C(xt,x0)))\begin{aligned} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \\ &\propto \exp \Big(-\frac{1}{2} \big(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\ &= \exp \Big(-\frac{1}{2} \big(\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \alpha_t} \color{red}{\mathbf{x}_{t-1}^2} }{\beta_t} + \frac{ \color{red}{\mathbf{x}_{t-1}^2} \color{black}{- 2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0} \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \bar{\alpha}_{t-1} \mathbf{x}_0^2} }{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\ &= \exp\Big( -\frac{1}{2} \big( \color{red}{(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2 - \color{blue}{(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1} \color{black}{ + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)} \end{aligned}

其中 C(xt,x0)C(\mathbf{x}_t, \mathbf{x}_0) 是和 xt−1\mathbf{x}_{t-1} 无关的常数。根据高斯分布的均值方差形式，通过配方法，上式可以参数化为：

β~t=1/(αtβt+11−αˉt−1)=1/(αt−αˉt+βtβt(1−αˉt−1))=1−αˉt−11−αˉt⋅βtμ~t(xt,x0)=(αtβtxt+αˉt−11−αˉt−1x0)/(αtβt+11−αˉt−1)=(αtβtxt+αˉt−11−αˉt−1x0)1−αˉt−11−αˉt⋅βt=αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉtx0\begin{aligned} \tilde{\beta}_t &= 1/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) = 1/(\frac{\alpha_t - \bar{\alpha}_t + \beta_t}{\beta_t(1 - \bar{\alpha}_{t-1})}) = \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\ \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0) &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) \\ &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0) \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\ &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\ \end{aligned}

此外，由于 x0=1αˉt(xt−1−αˉtϵt)\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t) ，带入上式可得：

μ~t=αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉt1αˉt(xt−1−αˉtϵt)=1αt(xt−1−αt1−αˉtϵt)\begin{aligned} \tilde{\boldsymbol{\mu}}_t &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t) \\ &= \color{cyan}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} \end{aligned}

自此关于扩散模型的前向扩散过程和逆扩散过程已经推导完毕。此时虽然我们有了形式化的逆扩散条件概率，但是其中的噪音量我们是不知道的。

在原 DDPM 论文中，逆扩散过程方差项为定值，均值项含噪音 ϵt\boldsymbol{\epsilon}_t，如果我们能够知道每一步的噪音，就可以去噪还原每一步的数据了，但它显然无法用公式求解，所以考虑：

  • 训练一个模型预测每一步的噪音，或者直接预测出每一步数据
  • 我们需要估计每个时刻的噪声，要恢复要去噪就要知道扩散过程究竟加了多少噪音
  • 模型的输入参数有两个：当前时刻 tt，和 xt\mathbf{x}_t ；ϵt\boldsymbol{\epsilon}_t 是噪声标签

简言之，前向过程就是提供噪声标签的过程。反向过程就是在拟合这个噪声。

为了设计一个合理的学习函数(损失函数)，观察使用网络 θ\theta 还原原数据 x0\mathbf{x}_0 过程中的对数似然变分下界：

−log⁡pθ(x0)≤−log⁡pθ(x0)+DKL(q(x1:T∣x0)∥pθ(x1:T∣x0))=−log⁡pθ(x0)+Ex1:T∼q(x1:T∣x0)[log⁡q(x1:T∣x0)pθ(x0:T)/pθ(x0)]=−log⁡pθ(x0)+Eq[log⁡q(x1:T∣x0)pθ(x0:T)+log⁡pθ(x0)]=Eq[log⁡q(x1:T∣x0)pθ(x0:T)]Let LVLB=Eq(x0:T)[log⁡q(x1:T∣x0)pθ(x0:T)]≥−Eq(x0)log⁡pθ(x0)\begin{aligned} - \log p_\theta(\mathbf{x}_0) &\leq - \log p_\theta(\mathbf{x}_0) + D_\text{KL}(q(\mathbf{x}_{1:T}\vert\mathbf{x}_0) \| p_\theta(\mathbf{x}_{1:T}\vert\mathbf{x}_0) ) \\ &= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_{\mathbf{x}_{1:T}\sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T}) / p_\theta(\mathbf{x}_0)} \Big] \\ &= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} + \log p_\theta(\mathbf{x}_0) \Big] \\ &= \mathbb{E}_q \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\ \text{Let }L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \geq - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0) \end{aligned}

这个结果看起来很突兀，实际上我们也可以从詹森不等式角度得到：

LCE=−Eq(x0)log⁡pθ(x0)=−Eq(x0)log⁡(∫pθ(x0:T)dx1:T)=−Eq(x0)log⁡(∫q(x1:T∣x0)pθ(x0:T)q(x1:T∣x0)dx1:T)=−Eq(x0)log⁡(Eq(x1:T∣x0)pθ(x0:T)q(x1:T∣x0))≤−Eq(x0:T)log⁡pθ(x0:T)q(x1:T∣x0)=Eq(x0:T)[log⁡q(x1:T∣x0)pθ(x0:T)]=LVLB\begin{aligned} L_\text{CE} &= - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \int p_\theta(\mathbf{x}_{0:T}) d\mathbf{x}_{1:T} \Big) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \int q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} d\mathbf{x}_{1:T} \Big) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \mathbb{E}_{q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \Big) \\ &\leq - \mathbb{E}_{q(\mathbf{x}_{0:T})} \log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \\ &= \mathbb{E}_{q(\mathbf{x}_{0:T})}\Big[\log \frac{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})}{p_\theta(\mathbf{x}_{0:T})} \Big] = L_\text{VLB} \end{aligned}

有了似然函数的界还不够，我们需要一个可解析计算的界来帮助我们设计损失函数，为了将上式中的每一项转化为可解析计算的，上式目标可以进一步重写为几个 KL 散度和熵项的组合：

LVLB=Eq(x0:T)[log⁡q(x1:T∣x0)pθ(x0:T)]=Eq[log⁡∏t=1Tq(xt∣xt−1)pθ(xT)∏t=1Tpθ(xt−1∣xt)]=Eq[−log⁡pθ(xT)+∑t=1Tlog⁡q(xt∣xt−1)pθ(xt−1∣xt)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt∣xt−1)pθ(xt−1∣xt)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡(q(xt−1∣xt,x0)pθ(xt−1∣xt)⋅q(xt∣x0)q(xt−1∣x0))+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)+∑t=2Tlog⁡q(xt∣x0)q(xt−1∣x0)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)+log⁡q(xT∣x0)q(x1∣x0)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[log⁡q(xT∣x0)pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)−log⁡pθ(x0∣x1)]=Eq[DKL(q(xT∣x0)∥pθ(xT))⏟LT+∑t=2TDKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))⏟Lt−1−log⁡pθ(x0∣x1)⏟L0]\begin{aligned} L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\ &= \mathbb{E}_q \Big[ \log\frac{\prod_{t=1}^T q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{ p_\theta(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) } \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=1}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \Big( \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\cdot \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1}\vert\mathbf{x}_0)} \Big) + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1} \vert \mathbf{x}_0)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{q(\mathbf{x}_1 \vert \mathbf{x}_0)} + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big]\\ &= \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \Big] \\ &= \mathbb{E}_q [\underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} + \sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ] \end{aligned}

LVLB=Eq[DKL(q(xT∣x0)∥pθ(xT))⏟LT+∑t=2TDKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))⏟Lt−1−log⁡pθ(x0∣x1)⏟L0]\begin{aligned} L_\text{VLB} = \mathbb{E}_q [\underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} + \sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ] \end{aligned}

让我们分别标记变分下界损失中的每个分量：

LVLB=LT+LT−1+⋯+L0where LT=DKL(q(xT∣x0)∥pθ(xT))Lt=DKL(q(xt∣xt+1,x0)∥pθ(xt∣xt+1)) for 1≤t≤T−1L0=−log⁡pθ(x0∣x1)\begin{aligned} L_\text{VLB} &= L_T + L_{T-1} + \dots + L_0 \\ \text{where } L_T &= D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T)) \\ L_t &= D_\text{KL}(q(\mathbf{x}_t \vert \mathbf{x}_{t+1}, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_t \vert\mathbf{x}_{t+1})) \text{ for }1 \leq t \leq T-1 \\ L_0 &= - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \end{aligned}

LTL_T 是常数，因为 TT 步的 xT\mathbf{x}_T 是纯高斯噪音，而 qq 无可学习参数。L0L_0 情况暂时忽略，总之可以当常数看。重点是 LtL_t 项。

从 LtL_t 到训练损失函数

回想一下，我们需要学习一个神经网络来近似逆向扩散过程中的条件概率分布：

pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))

方差项再 DDPM 中是定值，于是实际上是训练 μθ\boldsymbol{\mu}_\theta 来预测 μ~t=1αt(xt−1−αt1−αˉtϵt)\tilde{\boldsymbol{\mu}}_t = \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big) ，因为 xt\mathbf{x}_t 在训练中是已知的，实际上我们只需参数化噪声项：

μθ(xt,t)=1αt(xt−1−αt1−αˉtϵθ(xt,t))Thus xt−1=N(xt−1;1αt(xt−1−αt1−αˉtϵθ(xt,t)),Σθ(xt,t))\begin{aligned} \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) &= \color{cyan}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big)} \\ \text{Thus }\mathbf{x}_{t-1} &= \mathcal{N}(\mathbf{x}_{t-1}; \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) \end{aligned}

损失项 LtL_t 可以被写为最小化预测均值与真实均值之间的误差：

Lt=Ex0,ϵ[12∥Σθ(xt,t)∥22∥μ~t(xt,x0)−μθ(xt,t)∥2]=Ex0,ϵ[12∥Σθ∥22∥1αt(xt−1−αt1−αˉtϵt)−1αt(xt−1−αt1−αˉtϵθ(xt,t))∥2]=Ex0,ϵ[(1−αt)22αt(1−αˉt)∥Σθ∥22∥ϵt−ϵθ(xt,t)∥2]=Ex0,ϵ[(1−αt)22αt(1−αˉt)∥Σθ∥22∥ϵt−ϵθ(αˉtx0+1−αˉtϵt,t)∥2]\begin{aligned} L_t &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \| \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) \|^2_2} \| \color{blue}{\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - \color{green}{\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \|\boldsymbol{\Sigma}_\theta \|^2_2} \| \color{blue}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} - \color{green}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) \Big)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}

最终转换为噪声项之间的差值。

简化损失函数

根据经验，Ho等人发现，训练扩散模型使用忽略加权项的简化目标效果更好:

Ltsimple=Et∼[1,T],x0,ϵt[∥ϵt−ϵθ(xt,t)∥2]=Et∼[1,T],x0,ϵt[∥ϵt−ϵθ(αˉtx0+1−αˉtϵt,t)∥2]\begin{aligned} L_t^\text{simple} &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}

最终的损失函数：

Lsimple=Ltsimple+CL_\text{simple} = L_t^\text{simple} + C

其中 CC 为常数。

img

加速扩散模型采样 DDIM

由于DDPM加噪基于马尔科夫链过程，那么在去噪过程过程也必须基于这个过程，遵循马尔可夫链的逆扩散过程从 DDPM 生成样本非常慢。

DDPM 的损失函数 LsimpleL_{simple} 只依赖边缘分布 q(xt∣x0)q(\mathbf{x}_t \vert \mathbf{x}_{0}) 而不直接依赖联合分布 q(x1:T∣x0)q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0}) ，就是说联合分布形式并不影响我们训练 DDPM 的过程，DDPM 中联合分布恰好可以按马尔可夫性拆分为一个个条件分布，那么是否存在非马尔可夫的加噪过程，或者说更一般的加噪过程呢，确实存在，所以我们可以设计一种非马尔可夫加噪过程，并且我们能保证 q(xt∣x0)q(\mathbf{x}_t \vert \mathbf{x}_{0}) 与 DDPM 中保持一致，也就是训练可以共享同样的目标函数。换句话说，只要 q(xt∣x0)q(\mathbf{x}_t \vert \mathbf{x}_{0}) 已知并且是高斯分布，那么就可以使用 LsimpleL_{simple} 来训练模型。

在 DDPM 中，由于马尔可夫性，有 q(xt∣xt−1,x0)=q(xt∣xt−1)q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0)=q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) ，如果我们能够吧 q(xt∣xt−1,x0)q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) 推广到更一般的形式，并且保证 q(xt∣x0)q(\mathbf{x}_t \vert \mathbf{x}_0) 形式不变(高斯)，那么我们就能在不改变 DDPM 前提下，只需重写采样函数。

论文就给出了一种非马尔可夫前向扩散过程的公式和后验概率表达式，而该后验概率恰好满足 DDPM 中的边缘分布 q(xt∣x0)q(\mathbf{x}_t \vert \mathbf{x}_{0}) ：(证明略)

qσ(x1:T∣x0):=qσ(xT∣x0)Πt=2Tqσ(xt−1∣xt,x0)q_\sigma(\mathbf{x}_{1:T} \vert \mathbf{x}_0):=q_\sigma(\mathbf{x}_{T} \vert \mathbf{x}_0)\Pi_{t=2}^Tq_\sigma(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)

并且有 qσ(xt−1∣xt,x0)q_\sigma(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) ：

xt−1=αˉt−1x0+1−αˉt−1ϵt−1=αˉt−1x0+1−αˉt−1−σt2ϵt+σtϵ=αˉt−1x0+1−αˉt−1−σt2xt−αˉtx01−αˉt+σtϵqσ(xt−1∣xt,x0)=N(xt−1;αˉt−1x0+1−αˉt−1−σt2xt−αˉtx01−αˉt,σt2I)\begin{aligned} \mathbf{x}_{t-1} &= \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1}}\boldsymbol{\epsilon}_{t-1} \\ &= \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \boldsymbol{\epsilon}_t + \sigma_t\boldsymbol{\epsilon} \\ &= \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \frac{\mathbf{x}_t - \sqrt{\bar{\alpha}_t}\mathbf{x}_0}{\sqrt{1 - \bar{\alpha}_t}} + \sigma_t\boldsymbol{\epsilon} \\ q_\sigma(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_{t-1}; \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \frac{\mathbf{x}_t - \sqrt{\bar{\alpha}_t}\mathbf{x}_0}{\sqrt{1 - \bar{\alpha}_t}}, \sigma_t^2 \mathbf{I}) \end{aligned}

由于 q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\boldsymbol{\mu}}(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \mathbf{I})，所以：

β~t=σt2=1−αˉt−11−αˉt⋅βt\tilde{\beta}_t = \sigma_t^2 = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t

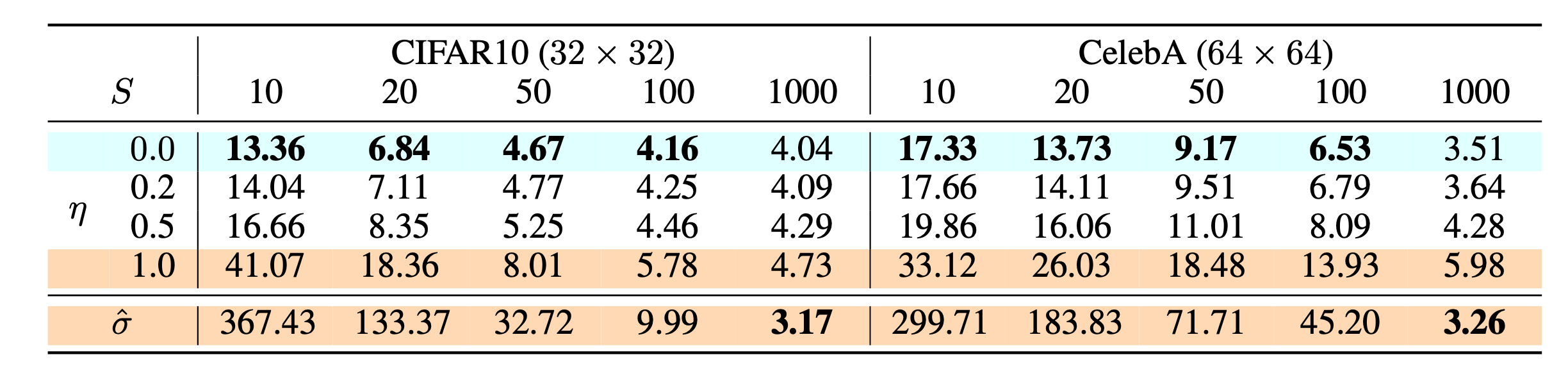
令 σt2=η⋅β~t\sigma_t^2 = \eta \cdot \tilde{\beta}_t ，于是我们可以调整 η∈R+\eta \in \mathbb{R}^+ 作为控制采样随机性的超参数，特殊地 η=0\eta=0 可使采样过程具有确定性。这就是 DDIM 名称的由来，它确定性地将噪声映射回原始数据样本。DDPM 中 η=1\eta=1 。

注意： 扩散模型加速采样的本质是提取预估了 x0x_0，用 x0x_0 算采样结果。

加速采样： respacing

在生成过程中，只需要采集 SS 步扩散 {τ1,…,τS}\{\tau_1, \dots, \tau_S\} 的子集，inference 过程变为子序列采样：

qσ,τ(xτi−1∣xτt,x0)=N(xτi−1;αˉt−1x0+1−αˉt−1−σt2xτi−αˉtx01−αˉt,σt2I)q_{\sigma, \tau}(\mathbf{x}_{\tau_{i-1}} \vert \mathbf{x}_{\tau_t}, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{\tau_{i-1}}; \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \frac{\mathbf{x}_{\tau_i} - \sqrt{\bar{\alpha}_t}\mathbf{x}_0}{\sqrt{1 - \bar{\alpha}_t}}, \sigma_t^2 \mathbf{I})

使用 DDIM，可以将扩散模型训练到任意数量的前向步骤，但在生成过程中只需要在步骤子集中进行采样即可。也就是我们不必在完整的时间序列进行解码过程，只需要在它的子序列上去做即可。

img

分数扩散模型 NCSN

D3PM

image-20230210150702089

参考文献

DDPM

DDIM

NCSN

Q.E.D.

我是星，利剑开刃寒光锋芒的银星，绝不消隐