二叉树
普通二叉树
后缀表达式
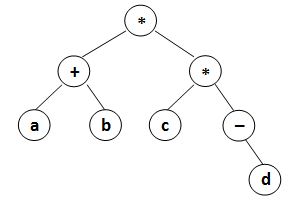
给定一个二叉表达式树,请你输出相应的后缀表达式,由于有单独的负号,添加括号表示优先级。AcWing4274
输入格式
第一行包含整数 ,表示节点数量。节点编号 。
接下来 行,每行给出一个节点的信息(第 行对应第 个节点),格式为:data left_child right_child。
其中,data 是一个不超过 个字符的字符串,left_child 和 right_child 分别是该节点的左右子节点的编号。没有子节点(即 NULL)用 表示。
输出格式
在一行中输出答案,表达式符号之间不得有空格。
样例:
输入样例:
8
* 8 7
a -1 -1
* 4 1
+ 2 5
b -1 -1
d -1 -1
- -1 6
c -1 -1
输出样例:
(((a)(b)+)((c)(-(d))*)*)
代码:
#include <iostream>
using namespace std;
const int N = 25;
int n;
string v[N];
int l[N], r[N];
int has_father[N];
void dfs(int u){
cout << '(';
if(l[u] != -1 && r[u] != -1){// 左右儿子都有,后序遍历
dfs(l[u]);
dfs(r[u]);
cout << v[u];
}else if(l[u] == -1 && r[u] == -1) cout << v[u];
else if(l[u] == -1 && r[u] != -1){//只有右儿子说明是负号
cout << v[u];
dfs(r[u]);
}
cout << ')';
}
int main(){
cin >> n;
for (int i = 1; i <= n; i ++ ){
cin >> v[i] >> l[i] >> r[i];
if (l[i] != -1) has_father[l[i]] = 1;
if (r[i] != -1) has_father[r[i]] = 1;
}
int root;
for (int i = 1; i <= n; i ++ ) if (!has_father[i]) root = i;
dfs(root);
return 0;
}
中缀表达式:AcWing1623
#include <iostream>
using namespace std;
const int N = 25;
int n;
string v[N];
int l[N], r[N];
int has_father[N];
string res;
void dfs(int u){
if(u == -1) return;
if(l[u] == -1 && r[u] == -1) res += v[u];
else{
res += '(';
dfs(l[u]);
res += v[u];
dfs(r[u]);
res += ')';
}
}
int main(){
cin >> n;
for(int i = 1; i <= n; i ++){
cin >> v[i] >> l[i] >> r[i];
if(l[i] != -1) has_father[l[i]] = 1;
if(r[i] != -1) has_father[r[i]] = 1;
}
int root;
for(int i = 1; i <= n; i ++) if(!has_father[i]) root = i;
dfs(root);
if(res.size() == 1) cout << res;
else cout << res.substr(1, res.size() - 2) << endl;
}
完全二叉树的最近公共祖先
编号从1开始的完全二叉树。AcWing3432
1
/ \
2 3
/ \ / \
4 5 6 7
/\ /\ /\ /\
... ...
代码:
#include <iostream>
using namespace std;
int main(){
int x, y; cin >> x >> y;
while(x != y){
if(x > y) x /= 2;
else y /= 2;
}
cout << x << endl;
return 0;
}
二叉树最近公共祖先
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1010;
int l[N], r[N], p[N];
int d[N];
void dfs(int u, int dist){
d[u] = dist;
if(l[u] != -1) dfs(l[u], dist + 1);
if(r[u] != -1) dfs(r[u], dist + 1);
}
int lca(int a, int b){
if(d[a] < d[b]) return lca(b, a);
while(d[a] > d[b]) a = p[a];
while(a != b) a = p[a], b = p[b];
return a;
}
int main(){
int t; cin >> t;
while(t --){
int n, m; cin >> n >> m;
for(int i = 1; i <= n; i ++) {
int left, right; cin >> left >> right;
l[i] = left, r[i] = right;
if(left != -1) p[left] = i;
if(right != -1) p[right] = i;
}
int root = 1;
while(p[root] != 0) root = p[root];
dfs(root, 0);
for(int i = 1; i <= m; i ++){
int a, b; cin >> a >> b;
int c = lca(a, b);
cout << d[a] + d[b] - 2 * d[c] << endl;
}
}
}
根能抵达的点的数量
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20010, M = N * 2;
int h[N], e[M], w[M], ne[M], idx;
int n, m;
void add(int a, int b, int c){
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u, int mid, int fa){
int res = 1;
for (int i = h[u]; ~i; i = ne[i]){
int j = e[i];
if (j == fa || w[i] < mid) continue;// 不能再访问父节点保证了遍历不会重复
res += dfs(j, mid, u);
}
return res;
}
int main(){
int T; cin >> T;
while (T -- ){
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
idx = 0;
for (int i = 0; i < n - 1; i ++ ){
int a, b, c; cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
int l = 0, r = 1e8;
while (l < r){
int mid = (l + r) >> 1;
if (dfs(0, mid, -1) <= m) r = mid;
else l = mid + 1;
}
cout << r << endl;
}
return 0;
}
前序中序求后序
#include <iostream>
using namespace std;
void dfs(string pre, string in){
if(pre.empty()) return;
char root = pre[0];
int k = in.find(root);
dfs(pre.substr(1, k), in.substr(0, k));
dfs(pre.substr(k + 1), in.substr(k + 1));
cout << root;
}
int main(){
string pre, in;
while(cin >> pre >> in){
dfs(pre, in);
cout << endl;
}
}
Q.E.D.